Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi K là giao điểm của AD và BC
\(\Rightarrow\) Tam giác KDC vuông tại K (do D+C=90) hay tam giác KAB vuông tại K
Gọi F là giao điểm của KM với CD
Áp dụng định lý Thales có:
\(\dfrac{AM}{DF}=\dfrac{KM}{KF}\)
\(\dfrac{KM}{KF}=\dfrac{MB}{FC}\)
\(\Rightarrow\dfrac{AM}{DF}=\dfrac{MB}{FC}\) mà AM=MB \(\Rightarrow DF=FC\)
\(\Rightarrow\) F là trung điểm của DC mà N cũng là tđ của DC
\(\Rightarrow F\equiv M\)
\(\Rightarrow\) K;M;N thẳng hàng
Áp dụng định lý Thales có:
\(\dfrac{KM}{KN}=\dfrac{AM}{DN}\Rightarrow\dfrac{KM}{AM}=\dfrac{KN}{DN}=\dfrac{KN-KM}{DN-AM}=\dfrac{MN}{\dfrac{1}{2}\left(DC-AB\right)}=\dfrac{2MN}{DC-AB}\)
Do đó \(\dfrac{KM}{AM}=\dfrac{2MN}{DC-AB}\)
Do M là tđ của AB mà tam giác KAB vuông tại K \(\Rightarrow KM=\dfrac{1}{2}AB\)
Lại có: \(AM=\dfrac{1}{2}AB\Rightarrow KM=AM\)\(\Rightarrow\dfrac{2MN}{DC-AB}=1\)
\(\Rightarrow MN=\dfrac{DC-AB}{2}\) (đpcm)

Gọi P là trung điểm của AD. Ta chứng minh được NP và MP lần lượt là đường trung bình của tam giác ABD và ADC nên suy ra NP//AB và MP//DC. Mặt khác AB//CD nên ta có P, N, M thẳng hàng MN//AB//DC
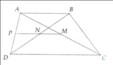

Kẻ AN cắt CD tại E
Xét △ANB và △END có :
^ANB = ^END (đối đỉnh)
NB = ND (gt)
^ABD = ^BDE (so le trong)
\(\Rightarrow\)△ANB = △END (g.c.g)
\(\Rightarrow\)AN = NE (cặp cạnh tương ứng)
Xét △AEC có : AM = MC
AN = NE
\(\Rightarrow\)MN // EC
\(\Rightarrow\)MN // AB // CD (ĐPCM)

a, gọi MN cắt BC tại O
xét tam giácBDC có : M là trung điểm của BD (gt)
MO // DC (Gt)
=> O là trung điểm của BC (đl)
xét tam giác ABC có : NO // AB
=> N là trung điểm của AB (đl)

a/
△ACD có:
- MN lần lượt đi qua trung điểm của AD và AC tại M và N
=> MN là đường trung bình của △ACD
Mặt khác, hình thang ABCD có:
- MP lần lượt đi qua trung điểm của AD và BC tại M và P
=> MP là đường trung bình của hình thang ABCD
=> MN trùng MP
Vậy: M, N, P thẳng hàng. (đpcm)
b/
- MN là đường trung bình của △ACD (cmt)
=> \(MN=\dfrac{1}{2}CD\)
Hay: \(MN=\dfrac{1}{2}.7=3,5\left(cm\right)\)
- MP là đường trung bình của hình thang ABCD (cmt)
=> \(MP=\dfrac{1}{2}AB.CD\)
Hay: \(MP=\dfrac{5+7}{2}=6\left(cm\right)\)
- \(NP=MP-MN\)
Hay: \(NP=6-3,5=2,5\left(cm\right)\)
- Nhận xét: Độ dài MP = 1/2 tổng độ dài hai đáy AB và CD
Vậy:
\(MN=3,5\left(cm\right)\)
\(NP=2,5\left(cm\right)\)
\(MP=6\left(cm\right)\)

mk ko hiu cau hoi cua pan
ai **** mình mình cho 3 ****