Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AB+CD=35,28*2:4,2=16,8(m)
CD-AB=8,4
=>CD=(16,8+8,4)/2=12,6 và AB=4,2
b: AD=2/3DE
=>DA=2/3DE
=>EA=1/3DE
Xét ΔEDC và ΔEAB có
góc E chung
góc EDC=góc EAB
=>ΔEDC đồng dạng với ΔEAB
=>S EDC/S EAB=(DC/AB)^2=4
=>S EAB/S EDC=1/4
=>S EAB/S ABCD=1/3
=>S EAB=1/3*35,28=11,76(cm2)

Ta có diện tích hình thang = (a + b) x h : 2 => để tìm tổng hai đáy ta có công thức: S x 2 : h
= > Tổng độ dài hai đáy:
29,34 x 2 : 3,6 = 16,3 m
a) Độ dài đáy lớn hơn đáy bé 7,5 m => Đây là hiệu hai đáy. Ta áp dụng dạng tổng - hiệu
Độ dài đáy lớn:
(16,3 + 7,5) : 2 = 11,9 m
Độ dài đáy bé:
16,3 - 11,9 = 4,4 m
b) (đợi chút)

Tổng độ dài đáy lớn và đáy bé của hình thang ABCD là:
29,43 x 2: 3,6 = 16,35 (m2)
Gọi độ dài đáy lớn là: \(x\) (m); \(x\) > 0
Thì độ dài đáy bé là: \(x\) - 7,5 (m)
Theo bài ra ta có phương trình: \(x\) + \(x\) - 7,5 = 16,35
2\(x\) = 16,35 + 7,5
2\(x\) = 23,85
\(x\) = 23,85:2
\(x\) = 11,925 (m)
Dộ dài đáy bé của hình thang ABCD là: 11,925 - 7,5 = 4,425 (m)
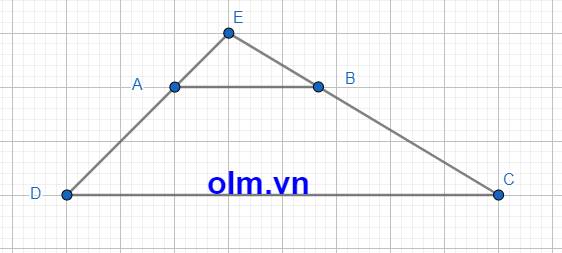
AE = DE - AD = \(\dfrac{3}{2}\)AD - AD = \(\dfrac{1}{2}\)AD
⇒SAEB = \(\dfrac{1}{2}\)SABD (Vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy DE và AE = \(\dfrac{1}{2}\)AD)
SABD = 4,425 x 3,6 : 2 = 7,965 (m2)
SABE = 7,965 : 2 = 3,9825 (m2)

Bài 1: Bài làm:
Chiều cao của hình thang là :
40 x 2 : 5 = 16 ( cm )
Diện tích của hình thang là :
( 27 + 48 ) x 16 : 2 = 600 ( cm2 )
Bài 2 Bài làm:
a, Tổng số phần bằng nhau là: 3+4=7 phần
Độ dài đáy là: 105:7x4=60 m
Chiều cao là: 105-60 =45 m
Diên tích là: 60x45=2700 m2
b, Độ dài đáy giảm 3 lần nên đáy mới là: 60:3=20 m
Chiều cao là: 1800:20=90 m
Chiều cao tăng là: 90:45=2 lần

a) Đáy lớn hình thang là:
8 + 6 = 14 cm
b) Chiều cao AH là:
( 6 + 8 ) : 2 = 7 cm
Diện tích hình thang ABCD là:
8 x 6 = 48 cm2
c) bạn tự làm nha!

AB=CD-6=16-6=10(cm)
\(AD=\dfrac{AB}{2}=5\left(cm\right)\)
Vì ABCD là hình thang cân
nên \(AD=BC=5\left(cm\right)\)
Chu vi hình thang cân ABCD là:
\(AB+AD+CD+BC=5+5+10+16=36\left(cm\right)\)
Diện tích hình thang cân ABCD là:
\(S_{ABCD}=\dfrac{1}{2}\cdot AH\cdot\left(AB+CD\right)\)
\(=\dfrac{1}{2}\cdot4\cdot\left(10+16\right)=2\cdot26=52\left(cm^2\right)\)
Cạnh AB dài:
16 - 6 = 10 (cm)
Cạnh AD dài:
10 : 2 = 5 (cm)
Chu vi hình thang cân ABCD:
16 + 10 + 5 + 5 = 36 (cm)
Diện tích hình thang:
(16 + 10) × 4 : 2 = 52 (cm²)
1: \(S_{ABCD}=\dfrac{1}{2}\cdot AH\cdot\left(AB+CD\right)\)
=>\(\left(AB+3AB\right)\cdot\dfrac{1}{2}\cdot3=30\)
=>4AB=20
=>AB=5(m)
CD=3*AB=15(m)
2:
Xét ΔEAB có AB//CD
nên \(\dfrac{EA}{ED}=\dfrac{AB}{CD}\)
=>\(\dfrac{EA}{ED}=\dfrac{1}{3}\)
Xét ΔEAB và ΔEDC có
\(\widehat{E}\) chung
\(\dfrac{EA}{ED}=\dfrac{EB}{EC}\)
Do đó: ΔEAB đồng dạng với ΔEDC
=>\(\dfrac{S_{EAB}}{S_{EDC}}=\left(\dfrac{AB}{DC}\right)^2=\dfrac{1}{9}\)
=>\(\dfrac{S_{EAB}}{S_{ABCD}}=\dfrac{1}{8}\)
=>\(S_{EAB}=\dfrac{30}{8}=3,75\left(m^2\right)\)