Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có Ab song song với Dc=> BAK=AKD
mà BAK=DAK( do Ak là tpg của DAB)
=> DAk=AKD=> tam giác DAk cân tại D=>DA=Dk(1)
chứng minh tương tự với tam giác BKC => tam giác BkC cân tại BKC cân tại C=> BC=KC(2)
Cộng (1),(2) => DA+BC=DK+KC
=> Da+Bc=DC
Lời nói chẳng mất tiền mua. Lựa lời mà chửi cho vừa lòng nhau. Đã chửi, phải chửi thật đau. Chửi mà hiền quá còn lâu nó chừa. Chửi đúng , không được chửi bừa . Chửi cha mẹ nó , không thừa một ai . Khi chửi , chửi lớn mới oai. Chửi hay là phải chửi dài , chửi lâu . Chửi đi chửi lại mới ngầu. Chửi nhiều cho nó nhức đầu , đau tai. Chửi xong nhớ nói bái bai . Phóng nhanh kẻo bị ăn chai vào mồm.

Câu hỏi của Thư Anh Nguyễn - Toán lớp 8 - Học toán với OnlineMath. Em tham khảo link này nhé!

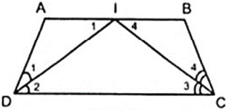
Áp dụng tính chất so le của AB//CD và giả thiết ta có:
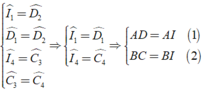
(vì trong một tam giác đối diện với hai góc bằng nhau là hai cạnh bằng nhau)
Cộng vế theo vế của ( 1 ) và ( 2 ) ta được: AD + BC = AB
Điều đó chứng tỏ tổng độ dài hai cạnh bên bằng độ dài của đáy AB của hình thang


a) Theo đề bài ta có: \(\widehat{DAF}+\widehat{ADF}=\frac{\widehat{DAB}+ADC}{2}=\frac{180^o}{2}=90^o\)
Xét tam giác AFD có \(\widehat{DAF}+\widehat{ADF}=90^o\) nên \(\widehat{AFD}=90^o\)
Hay tam giác AFD vuông tại F.
Gọi E là trung điểm AD.
Xét tam giác vuông ADF có FE là trung tuyến ứng với cạnh huyền nên EF = AD/2
Lại có do F là trung điểm BC; E là trung điểm AD nên EF là đường trung bình hình thang.
Từ đó suy ra \(EF=\frac{AB+BC}{2}\)
Vậy nên AD = AB + BC.
b) Giả sử AD = AE + ED.
Gọi E là trung điểm AD. Do AD = AB + CD nên FE = (AB + DC)/2
Ta có E là trung điểm AD. Vậy nên EF là đường trung bình hình thang hay hay Flà trung điểm BC.

Tham khảo : Câu hỏi của Trần Nhật Duy - Toán lớp 8 - Học toán với OnlineMath
nếu hình hơi bé bạn vào link này : https://hoc24.vn/images/discuss/1632366020_614bedc45d934.jpg