Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Gắn trục tọa độ Axyz với A là gốc tọa độ sao cho:
Tia Ax trùng tia AB; tia Ay trùng tia AD; tia Az trùng tia AS.
Khi đó:
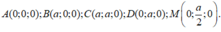
Gọi O là tâm hình vuông ABCD.
Do góc giữa mặt phẳng(SBD)và (ABCD) bằng 60 o nên S O A ⏞ = 60 o
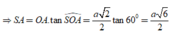
⇒ S 0 ; 0 ; a 6 2
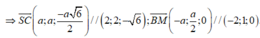
Mặt phẳng (P) chứa SC và song song với BM có vecto pháp tuyến là ( 6 ; 2 6 ; 6 ) / / 1 ; 2 ; 6 nên có phương trình:
x + 2 y + 6 z - 3 a = 0
Do đó: d ( S C , B M ) = d ( B ; ( P ) ) = 2 a 11 (đvđd).
Chọn D.
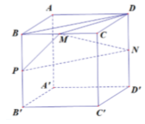
Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN). Do đó:
d(MN;BD) = d(BD;(MPN)) = d(B;(MPN))
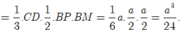
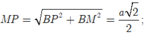
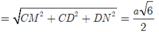
Nhận thấy 
nên tam giác MPN vuông tại M.
Do đó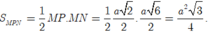 
Ta có 
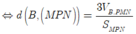
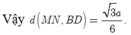
Cách 2:
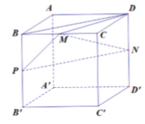
Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN).
Đồng thời, MP//CB', PN//B'D' => (MPN)//(CB'D')
Do đó 
(vì PC’ cắt B’C tại trọng tâm tam giác BB’C’).
Nhận thấy tứ diện C'.CB'D' là tứ diện vuông tại C' nên
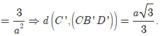
Vậy 
Cách 3: Tọa độ hóa
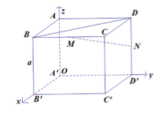
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó,
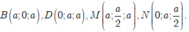
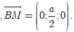
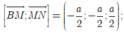
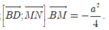
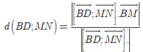
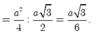
đáp án D
Do S.ABCD là hình chóp tứ giác đều ⇒ S O ⊥ ( A B C D ) .
Gọi K là trung điểm OD
MK sẽ là đường trung bình trong tam giác ∆ S O D
⇒ M K ⊥ ( A B C D )
⇒ tan M B K = M K B K
⇒ tan M B K = M K B K = 1 3
Chọn đáp án D
