Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

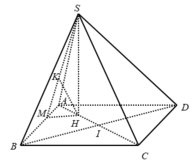
- Ta có: CD // AB nên CD// mp (SAB)
⇒ Suy ra:

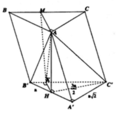
- Kẻ MH ⊥ AB, HK ⊥ SM.
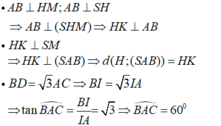
- Do đó, tam giác ABC là tam giác đều.
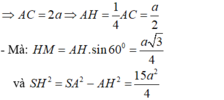
- Xét tam giác SHM vuông tại H; đường cao HK có:
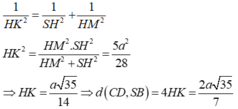

Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)
\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)
\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)
\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)
\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)
Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
\(HE=CH.sin30^0=\dfrac{a}{2}\)
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)

Ta có: BD = A’B = A’D nên tam giác A’BD là tam giác đều.
Lại có: AB = AD = AA’ nên hình chiếu vuông góc của điểm A lên mp(A’BD) là tâm của tam giác BDA’.
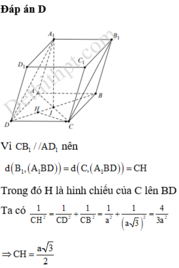
Đáp án D

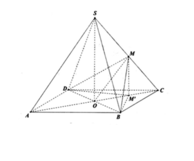
Do tam giác SAB cân và I là trung điểm AB \(\Rightarrow SI\perp AB\)
Mặt khác AB là giao tuyến của hai mặt phẳng vuông góc (SAB) và (ABCD)
\(\Rightarrow SI\perp\left(ABCD\right)\)
\(\Rightarrow SI\perp AD\) (1)
Lại có \(AD\perp AB\) (2) (giả thiết)
(1);(2)\(\Rightarrow AD\perp\left(SAB\right)\)
Mà \(AD\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(SAB\right)\)
b.
Theo cmt ta có \(\left\{{}\begin{matrix}SI\perp\left(ABCD\right)\\SI\in\left(SID\right)\end{matrix}\right.\) \(\Rightarrow\left(SID\right)\perp\left(ABCD\right)\)
c.
\(\overrightarrow{ID}.\overrightarrow{CK}=\left(\overrightarrow{IA}+\overrightarrow{AD}\right)\left(\overrightarrow{CD}+\overrightarrow{DK}\right)=\left(-\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\right)\left(-\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\right)\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}AD^2+\dfrac{1}{4}\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}AD^2\) (do AB vuông góc AD nên \(\overrightarrow{AB}.\overrightarrow{AD}=0\))
\(=0\) (ABCD là hình vuông nên AB=AD)
\(\Rightarrow ID\perp CK\)
Mà \(SI\perp\left(ABCD\right)\Rightarrow SI\perp CK\)
\(\Rightarrow CK\perp\left(SID\right)\)
\(\Rightarrow\left(SKC\right)\perp\left(SID\right)\)

Đáp án D
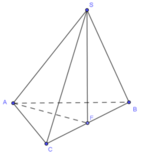
Góc giữa cạnh SA và đáy là S A F ^ ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
![]()
Vậy ![]()
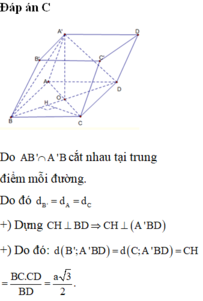
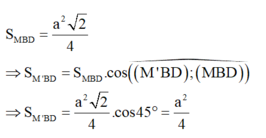
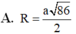
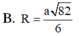

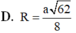
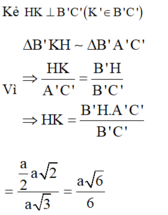


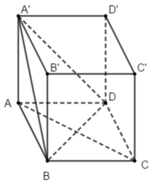

Gọi M là trung điểm của BD, là trung điểm của A’B.
Suy ra tâm O của tam giác BDA’ là giao của DN và A’M
Phương án D đúng vì BD ⊥ (AMA') bởi BD ⊥ AM và BD ⊥ A’M ⇒ BD ⊥ AO
BA’ ⊥ (AND) do BA’ ⊥ DN và A’B ⊥ AN ⇒ A’B ⊥ AO
AO ⊥ (A’BD) ⇒ O là hình chiếu của A trên (A’BD).
Đáp án D