

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Cho lăng trụ tam giác đều ABC.A'B'C'.
Gọi G, G; lần lượt là tâm của hai đáy ABC và A'B'C'.
Ta có GG' chính là trục của các tam giác ABC và A'B'C' .
Gọi O là trung điểm của GG' thì O cách đều 6 đỉnh của hình lăng trụ
nên là tâm của mặt cầu ngoại tiếp hình lăng trụ. Bán kính mặt cầu là R = OA.
Xét tam giác OAG vuông tại G, ta có:
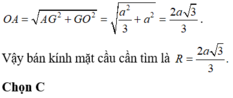

Đáp án B
Ta có mặt bên là hình chữ nhật có diện tích bằng 3 a 2
⇒ chiều cao của lăng trụ là 3 a 2 a = 3 a .
Có diện tích đáy hình trụ bằng S = πa 2
Vậy V = 3 a . πa 2 = 3 πa 2 .

Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và \(AH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Áp dụng định lý Pitago cho tam gaics vuông AA'H:
\(A'H=\sqrt{A'A^2-AH^2}=\dfrac{3a}{2}\)
\(V=A'A.S_{ABC}=\dfrac{3a}{2}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{3}}{8}\)