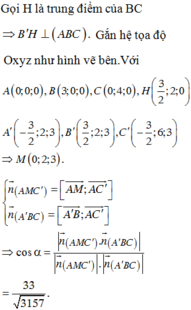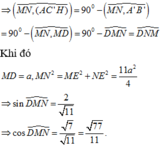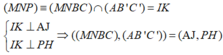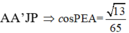Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.

Dễ thấy:
A B ' C ' ; M N P ^ = A B ' C ' ; M N C B ^
= 180 0 − A B ' C ' ; A ' B ' C ' ^ − M N B C ; A ' B ' C ' ^ = 180 0 − A ' B C ; A B C ^ − M N B C ; A B C . ^
Ta có:
M N B C ; A B C ^ = A ' P ; A P ^ = A ' P A ^ = arctan 2 3 .
Và
M N B C ; A B C ^ = S P ; A P ^ = S P A ^ = arctan 4 3 ,
với S là điểm đối xứng với A qua A’,
thì S A = 2 A A ' = 4.
Suy ra
cos A B ' C ' ; M N P ^ = c os 180 0 -arctan 2 3 − arctan 4 3 = 13 65 .

Đáp án A.
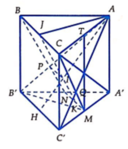
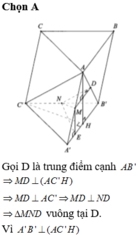
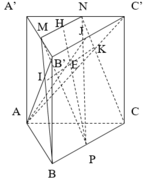
Cách 1: Gọi P là giao điểm của BN và A'B'=>P là trọng tâm Δ A ' B ' B .
Q là giao điểm của CM và A'C'=>Q là trọng tâm Δ A ' C ' C
⇒ P Q / / B ' C ' Ta có A B ' C ' ∩ B C M N = P Q .
Gọi H là trung điểm của B'C' và I là giao điểm của AH và PQ.
I là trung điểm của PQ.
Qua I kẻ đường thẳng vuông góc với BC, cắt BC và MN lần lượt tại J và K
=>J là trung điểm BC và K là trung điểm MN.
Ta có A B ' = A C ' ⇒ Δ A B ' C ' cân tại A ⇒ A H ⊥ B C ⇒ A I ⊥ P Q .
Lại có I J ⊥ P Q ⇒ Góc giữa A B ' C ' và B C M N là góc giữa IJ và IA.
Ta có:
A C ' = A C 2 + C C ' 2 = 2 3 2 + 2 2 = 4
⇒ A H = A C ' 2 − H C ' 2 = 4 2 − 3 2 = 13 ⇒ A I = 2 3 A H = 2 13 3
B N = B B ' 2 + B ' N 2 = 2 2 + 3 2 = 7
K J = N E = B N 2 − E B 2 = 7 − 3 4 = 5 2 ⇒ I J = 2 3 K J = 5 3
Lại có A J = 2 3 . 3 2 = 3
Trong Δ A I J :
cos A I J ^ = I J 2 + I A 2 − A J 2 2. I J . I A = 25 9 + 4.13 9 − 9 2. 5 3 . 2 13 3 = − 13 65 .
Cosin của góc giữa A B ' C ' và B C M N là 13 65
Cách 2: (Tọa độ hóa)
Gọi T là trung điểm AC. Đặt M = 0 ; 0 ; 0 , B ' 3 ; 0 ; 0 , C ' 0 ; 3 ; 0 , T 0 ; 0 ; 2
⇒ A 0 ; − 3 ; 2 , B 3 ; 0 ; 2 , C 0 ; 3 ; 2 ⇒ M B → = 3 ; 0 ; 2 , M C → = 0 ; 3 ; 2
n → = M B → , M C → = 2 3 ; 6 ; 6 3 là một vecto pháp tuyến của .
Lại có A B ' → = 3 ; 3 ; − 2 , A C ' → = 0 ; 2 3 ; − 2
⇒ n ' → = A B → , A C → ' = 2 3 ; 6 ; 6 3 là một vecto pháp tuyến của A B ' C ' .
Gọi α là góc giữa A B ' C ' và M N B C .
Ta có:
cos α = cos n → ; n ' → ^ = − 2 3 .2 3 + − 6 .6 + 3 3 .6 3 − 2 3 2 + − 6 2 + 3 3 2 . 2 3 2 + 6 2 + 6 3 2 = 13 65

Chọn đáp án D
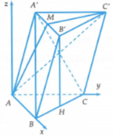
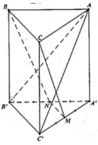
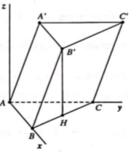
Gọi H là trung điểm của cạnh BC. Suy ra B ' H ⊥ A B C
∆ A B C vuông tại A nên B C = A B 2 + A C 2 = 5
vuông tại H nên B ' H = B ' B 2 - B H 2 = 3
Chọn hệ trục tọa độ Oxyz như hình, trong đó A ≡ O 0 ; 0 ; 0 , B 3 ; 0 ; 0 , C 0 ; 4 ; 0 .
Ta có H là trung điểm của BC nên H 3 2 ; 2 ; 0 , H là hình chiếu của B’ trên bề mặt phẳng (ABC) nên B ' 3 2 ; 2 ; 3 .
Từ A B ⇀ = A ' B ' ⇀ suy ra
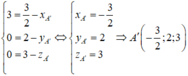
Từ A C ⇀ = A ' C ' ⇀ suy ra
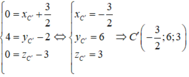
M là trung điểm của A’B’ nên M(0;2;3).
Ta có
![]()
![]()
Mặt phẳng (AMC’) có một vectơ pháp tuyến là n 1 ⇀ = 8 ; 3 ; - 2 .
Lại có A ' B ⇀ = 9 2 ; - 2 ; - 3 , A ' C ⇀ = 3 2 ; 2 ; - 3
⇒ A ' B ⇀ , A ' C ⇀ = 12 ; 9 ; 12
⇒ Mặt phẳng (A’BC) có một vectơ pháp tuyến là n 2 ⇀ = 4 ; 3 ; 4 .
Gọi α là góc tạo bởi hai mặt phẳng (AMC’) và (A’BC) thì:
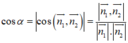
⇒ cos α = 33 3157

Dùng phương pháp tọa độ hóa.
Đặt hệ trục tọa độ, ở đây như thầy đã trình bày ta nên chọn gốc tại P trục Ox, Oy là PA và PC.
Gọi α góc tạo bởi hai mặt phẳng ( AB'C' ) và (MNP)
Khi đó cos α = n 1 → . n 2 → n 1 → . n 2 → = 13 65
Đáp án cần chọn là B

Đáp án D.
Phương pháp : Dựng thiết diện, xác định hai phần cần tính thể tích.
Sử dụng phân chia và lắp ghép các khối đa diện.
Cách giải : Gọi E = MN ∩ B'C'
Kéo dài MP cắt AB tại D, cắt AA ‘ tại F.
Nối NF, cắt AC tại G.
Do đó thiết diện của lăng trụ khi cắt bởi mặt phẳng (MNP) là NEPDG.
Gọi V1 là thể tích khối đa diện chứa đỉnh A’ ta có :
![]()
Ta có: ![]()
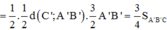
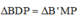
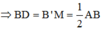
=> D là trung điểm của AB
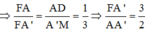
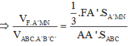
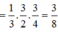
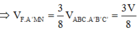
Dễ dàng chứng minh được ∆ADG đồng dạng ∆A’MN theo tỉ số 1 3
![]()
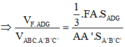
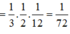
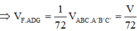
Áp dụng định lí Menelaus trong tam giác A’B’C’ ta có:
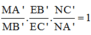
![]()
Áp dụng định lí Menelaus trong tam giác A’MN ta có:
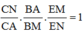
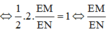
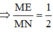
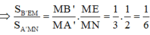
![]()
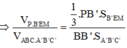
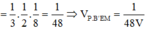
Vậy 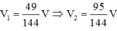
=> V 1 V 2 = 49 95