Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
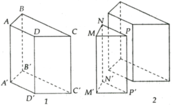
$AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-16^2}=12$ (cm)
Diện tích đáy là: $(12.16):2=96$ (cm2)
Diện tích toàn phần:
$S=p_{đáy}.h+2S_{đáy}=(16+12+20).12+2.96=768$ (cm2)
Thể tích lăng trụ:
$V=S_{đáy}.h=96.12=1152$ (cm3)

a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
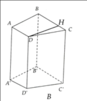
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2

\(BC=\sqrt{4^2-3^2}=\sqrt{7}\left(cm\right)\)
\(S_{Xq}=\left(3+\sqrt{7}\right)\cdot5=15+5\sqrt{7}\left(cm^2\right)\)
\(V=3\cdot\sqrt{7}\cdot5=15\sqrt{7}\left(cm^3\right)\)

Áp dụng định lí Py - Ta - Go , độ dài cạnh còn lại của mặt đáy tam giác là :
\(\sqrt{3^2+4^2}=5\left(cm\right)\)
Diện tích xung quanh hình lăng trụ đứng :
\(S_{xq}=\left(3+4+5\right).8=96\left(cm^2\right)\)
Diện tích toàn phần :
\(S_{tp}=96+\left(3.4\right)=108\left(cm^2\right)\)
Thể tích :
\(V=\dfrac{3.4}{2}.8=48\left(cm^3\right)\)