Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

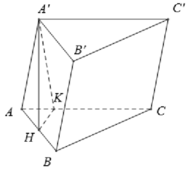
Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và \(AH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Áp dụng định lý Pitago cho tam gaics vuông AA'H:
\(A'H=\sqrt{A'A^2-AH^2}=\dfrac{3a}{2}\)
\(V=A'A.S_{ABC}=\dfrac{3a}{2}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{3}}{8}\)

Đáp án D
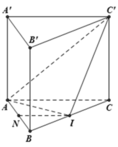
Gọi H là trung điểm của BC, khi đó từ giả thiết ta có A'H ⊥ (ABC). Ta có:
A'H = a 3 => V A . BCC ' B ' = V ABC . A ' B ' C ' - V A ' . ABC
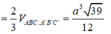

Đáp án D
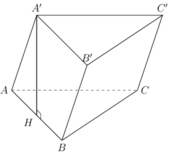
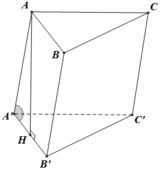
Ta có góc giữa cạnh bên AA' với mặt đáy (ABC) là:
góc A ' A H ^ và tan A ' A H = A ' H A H
Suy ra A ' H = a 2 . tan 30 ° = a 3 6
Do đó V = A ' H . S A B C = a 3 6 . a 2 3 4 = a 3 8
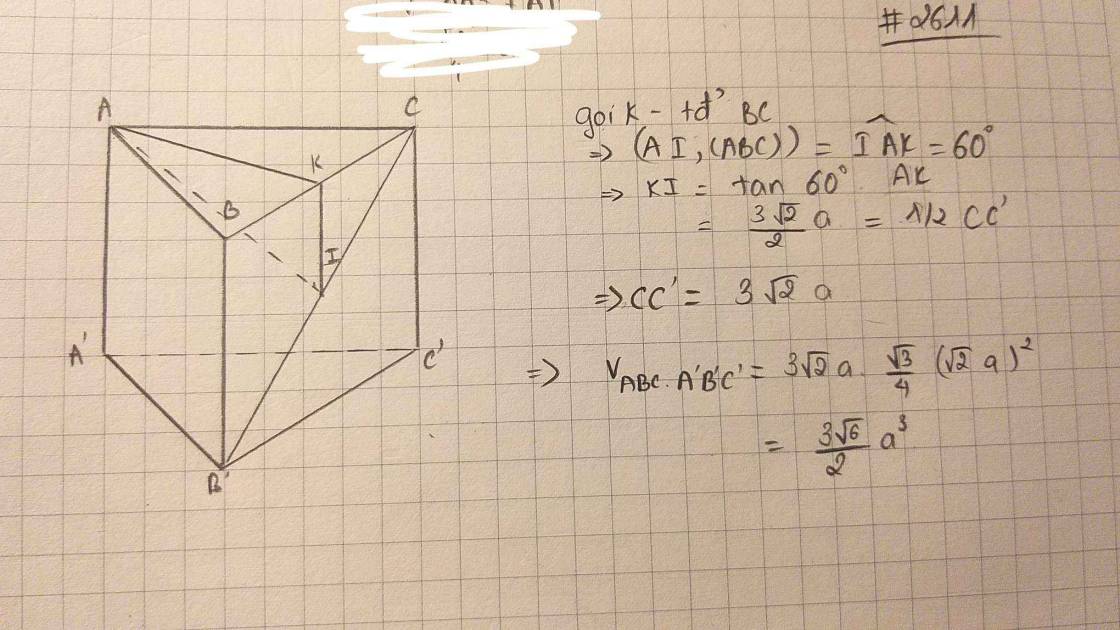




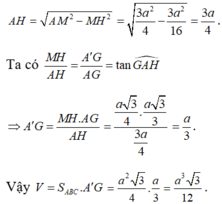
Đáp án C