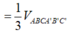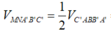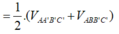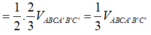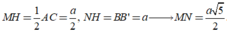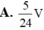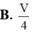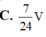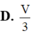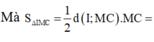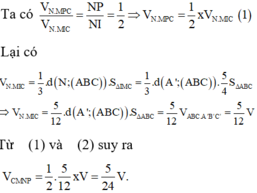Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

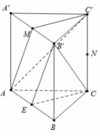
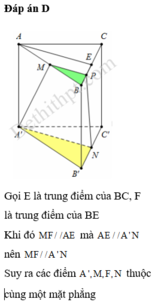
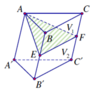
Gọi D, E, F lần lượt là trung điểm A'A, BC và MN
\(\left\{{}\begin{matrix}MN||B'C'\\DN||AB'\end{matrix}\right.\) (đường trung bình tam giác) \(\Rightarrow\left(AB'C'\right)||\left(DNM\right)\)
\(\Rightarrow\) Góc giữa (AB'C') bằng góc giữa (DNM) và (BCMN)
\(MN\perp A'F\) (A'MN là tam giác đều), và \(A'A\perp\left(A'B'C'\right)\Rightarrow A'A\perp MN\)
\(\Rightarrow MN\perp\left(A'AEF\right)\) \(\Rightarrow\) góc giữa (DNM) và (BCMN) là \(\widehat{DFE}\) nếu nó là góc nhọn và \(180^0-\widehat{DFE}\) nếu nó là góc tù
\(MN=\dfrac{1}{2}B'C'=\sqrt{3}\Rightarrow A'F=\dfrac{MN\sqrt{3}}{2}=\dfrac{3}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow DF=\sqrt{A'F^2+A'D^2}=\dfrac{\sqrt{13}}{2}\)
\(AE=\dfrac{AB\sqrt{3}}{2}=3\Rightarrow DE=\sqrt{AD^2+AE^2}=\sqrt{10}\)
Gọi G là trung điểm AE \(\Rightarrow FG\perp\left(ABC\right)\Rightarrow\left\{{}\begin{matrix}FG=A'A=2\\GE=\dfrac{1}{2}AE=\dfrac{3}{2}\end{matrix}\right.\)
\(EF=\sqrt{FG^2+EG^2}=\dfrac{5}{2}\)
Áp dụng định lý hàm cos:
\(cos\widehat{DFE}=\dfrac{DF^2+EF^2-DE^2}{2DF.EF}=...\Rightarrow\widehat{DFE}=...\)

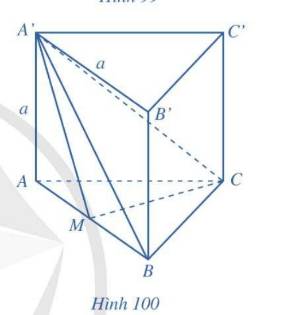
a) \(BCC'B'\) là hình chữ nhật \( \Rightarrow BC\parallel B'C'\)
\( \Rightarrow \left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^ \circ }\).
b)
\(\Delta AA'B\) vuông tại \(A \Rightarrow \tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
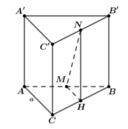
c) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot BC,CC' \bot CM\)
Vậy \(\widehat {BCM}\) là góc nhị diện \(\left[ {B,CC',M} \right]\).
\(\Delta ABC\) đều \( \Rightarrow \widehat {BCM} = \frac{1}{2}\widehat {ACB} = {30^ \circ }\).
d) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right)\)
\(\Delta ABC\) đều \( \Rightarrow CM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\left. \begin{array}{l}CC'\parallel AA'\\AA' \subset \left( {ABB'A'} \right)\end{array} \right\} \Rightarrow CC'\parallel \left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC',\left( {ABB'A'} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right) \Rightarrow CM \bot A'M\)
\(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot CM\)
\( \Rightarrow d\left( {CC',A'M} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
g) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4},h = AA' = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}\)
\({S_{\Delta MBC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{8},h = AA' = a\)
\( \Rightarrow {V_{A'.MBC}} = \frac{1}{3}{S_{\Delta MBC}}.AA' = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{8}.a = \frac{{{a^3}\sqrt 3 }}{{24}}\)

.a
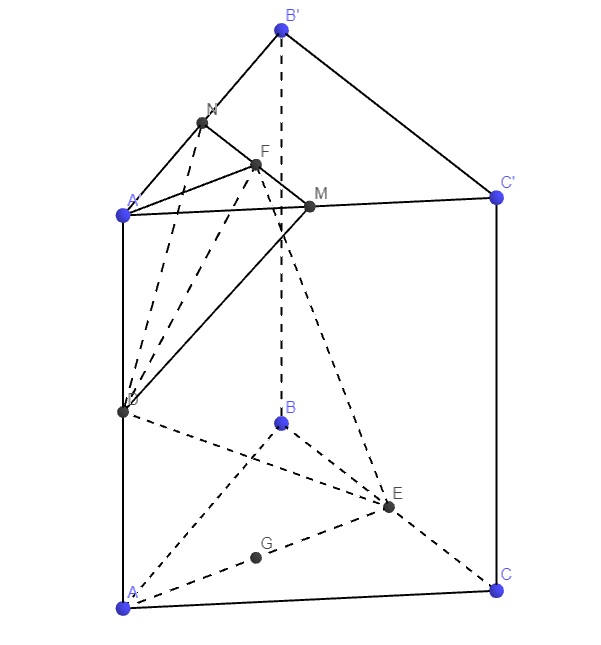
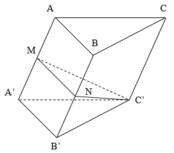
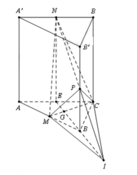
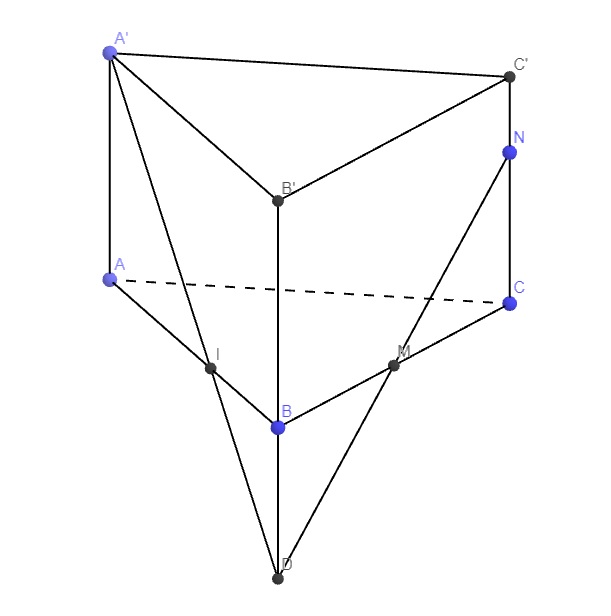
Trong mp (BCC'B') nối MN kéo dài cắt BB' tại D
\(\Rightarrow D\in\left(A'MN\right)\)
Trong mp (ABB'A') nối A'D cắt AB tại I
\(\Rightarrow I=AB\cap\left(A'MN\right)\)
Do CN song song BD, áp dụng Talet:
\(\dfrac{CN}{BD}=\dfrac{CM}{BM}=1\Rightarrow CN=BD\)
\(\Rightarrow\dfrac{BD}{BB'}=\dfrac{CN}{CC'}=\dfrac{2}{3}\)
Do AA' song song BD, áp dụng Talet:
\(\dfrac{IA}{IB}=\dfrac{AA'}{BD}=\dfrac{BB'}{BD}=\dfrac{3}{2}\)
Các câu này quá nhiều đường nét nên mỗi câu 1 hình riêng cho dễ nhìn:
b.
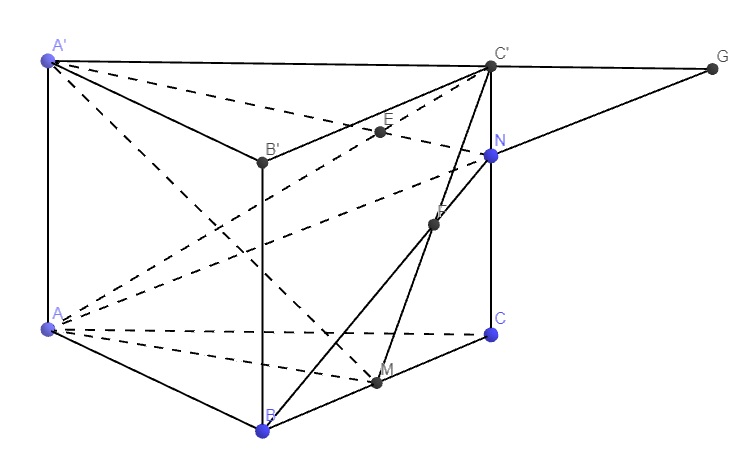
Trong mp (ACC'A'), gọi E là giao điểm A'N và AC'
Trong mp ((BCC'B'), gọi F là giao điểm BN và C'M
\(\Rightarrow EF=\left(AMC'\right)\cap\left(A'NB\right)\)
c.
Trong mp (ACC'A'), kéo dài AN và A'C' cắt nhau tại G
\(\Rightarrow G\in\left(ANB\right)\cap\left(MA'C'\right)\)
\(F=BN\cap C'M\Rightarrow F\in\left(ANB\right)\cap\left(MA'C'\right)\)
\(\Rightarrow FG=\left(ANB\right)\cap\left(MA'C'\right)\)

Đáp án C
Dễ thấy VA.BCC’B’ = 1 2 VABC.A’B’C’
Lại có VA.BCFE = 1 2 VA.BCC’B’
=> VA.BCFE = . VABC.A’B’C’