Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Phương pháp:
Lập tỉ số thể tích khối tứ diện ABCM và khối lăng trụ ABC.A’B’C’. Từ đó tính thể tích khối tứ diện ABCM.
Cách giải:
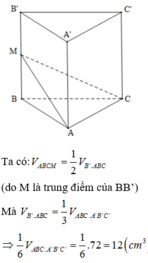


Sử dụng công thức tính thể tích khối chóp V = 1 3 h . S với h là chiều cao hình chóp và S là diện tích đáy.
Công thức tính thể tích lăng trụ V = h.S với h là chiều cao hìnhlăng trụ và S là diện tích đáy.
Cách giải:
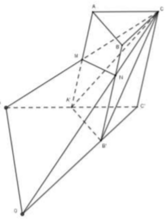

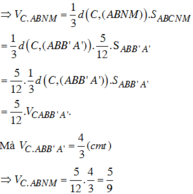
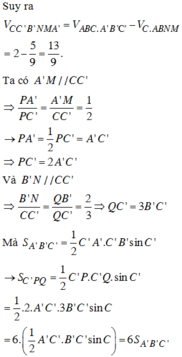
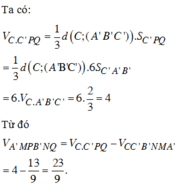

Đáp án B
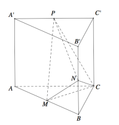
Vì M,N lần lượt là trung điểm của BB' và CC' nên ta có:
S M N C ' B ' = 1 2 S B C C ' B ' ⇒ V A ' . M N C ' B ' = 1 2 V A ' . B C C ' B ' = 1 2 V A B C . A ' B ' C ' - V A ' . A B C
Lại có:
V A ' . A B C = 1 3 V A B C . A ' B ' C ' ⇒ V A ' . M N C ' B ' = 1 2 V A B C . A ' B ' C ' - 1 3 V A B C . A ' B ' C ' = 1 3 V A B C . A ' B ' C '
Vậy tỉ số V 1 V 2 = V A ' M N A B C V A ' . M N C ' B ' = V A B C . A ' B ' C ' - 1 3 V A B C . A ' B ' C ' 1 3 V A B C . A ' B ' C ' = 2

Chọn B.
Phương pháp:

+) So sánh diện tích hình thang BMNC và diện tích hình bình hành BCC’B’ từ đó suy ra tỉ số thể tích V A . B M N C V A . B C C ' B '
+) So sánh V A . B C C ' B ' với V.
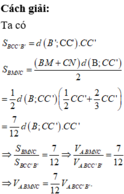
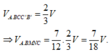

Đáp án B
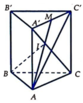
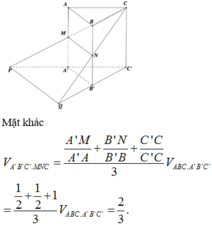
Xét ∆ A A ' C có I là trọng tâm, d ( I , ( A B C ) ) = 2 3 d ( M , ( A B C ) )
Ta có: V A B C . A ' B ' C ' = S A B C . A A ' = S A B C . d A ' ; A B C
V I A B C = 1 3 S ∆ A B C . d I , ( A B C ) = 1 3 S ∆ A B C . 2 3 d ( M , ( A B C ) ) = 2 9 S ∆ A B C . d ( A ' , ( A B C ) )

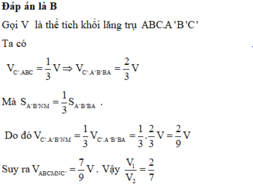

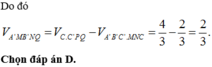

Đáp án A