Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

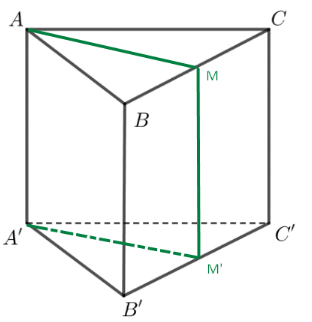
Ta có M, M' lần lượt là trung điểm của BC, B'C', BCC'B' là hình bình hành suy ra MM' // CC'.
Vì các cạnh bên của hình lăng trụ ABC.A'B'C' đôi một song song nên AA'//CC'.
Mặt phẳng ((AMC) //(A'M'C') nên AMC. AM'C' là hình lăng trụ.

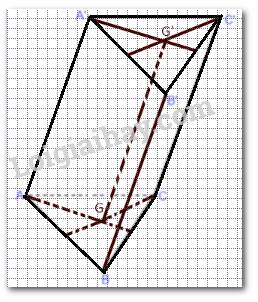
a) Ta có ABC.A'B'C' là hình lăng trụ nên \(\Delta ABC = \Delta A'B'C'\) suy ra AG = A'G'.
Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'.
Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành.
b) AGG'A' là hình bình hành suy ta AA' // GG'.
Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ).
Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ.

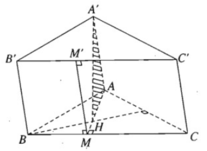
a) BC ⊥ AH và BC ⊥ A'H vì A'H ⊥ (ABC)
⇒ BC ⊥ (A'HA) ⇒ BC ⊥ AA'
Và B'C' ⊥ AA' vì BC // B'C'
b) Ta có AA' // BB' // CC' mà BC ⊥ AA' nên tứ giác BCC’B’ là hình chữ nhật. Vì AA' // (BCC'B') nên ta suy ra MM' ⊥ BC và MM' ⊥ B'C' hay MM’ là đường cao của hình chữ nhật BCC’B’.

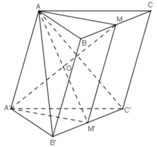
a) Do ABC.A’B’C’ là hình lăng trụ nên ta có: BCC’B’ là hình bình hành
Xét tứ giác BCC’B’ có M và M’ lần lượt là trung điểm của BC và B’C’ nên MM’ là đường trung bình
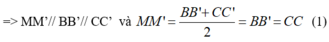
Lại có: AA’// BB’ và AA’= BB’ ( tính chất hình lăng trụ) (2)
Từ (1) và (2) suy ra: MM’// AA’ và MM’ = AA’
=> Tứ giác AMM’A’ là hình bình hành
b) Trong (AMM’A’) gọi O = A’M ∩ AM’, ta có :
Ta có : O ∈ AM’ ⊂ (AB’C’)
⇒ O = A’M ∩ (AB’C’).
c)
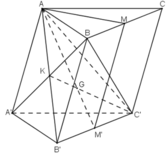
Gọi K = AB’ ∩ BA’, ta có :
K ∈ AB’ ⊂ (AB’C’)
K ∈ BA’ ⊂ (BA’C’)
⇒ K ∈ (AB’C’) ∩ (BA’C’)
Dễ dàng nhận thấy C’ ∈ (AB’C’) ∩ (BA’C’)
⇒ (AB’C’) ∩ (BA’C’) = KC’.
Vậy d cần tìm là đường thẳng KC’
d) Trong mp(AB’C’), gọi C’K ∩ AM’ = G.
Ta có: G ∈ AM’ ⊂ (AM’M)
G ∈ C’K.
⇒ G = (AM’M) ∩ C’K.
+ K = AB’ ∩ A’B là hai đường chéo của hình bình hành ABB’A’
⇒ K là trung điểm AB’.
ΔAB’C’ có G là giao điểm của 2 trung tuyến AM’ và C’K
⇒ G là trọng tâm ΔAB’C’.

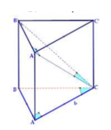

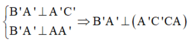
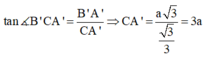
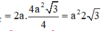
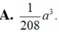
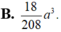
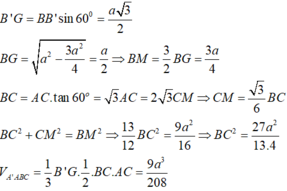

Ta có:
+ BB’ vuông góc với (ABC)
+ AH thuộc (ABC)
=> AH vuông góc với BB’
+ CC’ vuông góc (ABC)
+ AH thuộc (ABC)
=> AH vuông góc với CC’
Xét (BB’C’C) có:
+ AH vuông góc với BB’
+ AH vuông góc với CC’
=> AH vuông góc với (BB’C’C)
Mà B’C’ thuộc (BB’C’C)
=> AH vuông góc với B’C’