Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
c) Ta có DE // HM (cmt) ⇒ MHDE là hình thang (1)
Lại có HE = AC/2 (tính chất đường trung tuyến của tam giác vuông AHC)
DM = AC/2 (DM là đường trung bình của ΔABC) ⇒ HE = DM (2)
Từ (1) và (2) ⇒ MHDE là hình thang cân.
d) Gọi I là giao điểm của AH và DE. Xét ΔAHB có D là trung điểm của AB, DI // BH (cmt) ⇒ I là trung điểm của AH
Xét ΔDIH và ΔKIA có
IH = IA
∠DIH = ∠AIK (đối đỉnh),
∠H1 = ∠A1(so le trong)
ΔDIH = ΔKIA (g.c.g)
⇒ ID = IK
Tứ giác ADHK có ID = IK, IA = IH (cmt) ⇒ DHK là hình bình hành
⇒ HK // DA mà DA ⊥ AC ⇒ HK ⊥ AC

(Hình Tự vẽ)
Vì tam giác ABC có \(\widehat{A}=90\)
Mà AE là đường trung tuyến ( Vì E là trung điểm BC )
nên AE là đường trung tuyến ứng với cạnh huyễn
Suy ra \(AE=\frac{BC}{2}\)
hay AE = BE=EC (1)
Mà AE=ED (2)
Từ (1), và (2) suy ra AE=EB=EC=ED
Vì tứ giác ABDC có các đường chéo cắt nhau tại trung điểm mỗi đường và chúng đều bằng nhau
nên ABCD là hình chữ nhật
b, Vì EB=EC;FB=FK
nên EF là đường trung bình tam giác KBC
Suy ra EF//AC (1)
và EF=KC/2=AK=AC(2)
Từ (1) và (2) suy ra EF//AC VÀ EF=AC
Vậy ACEF là hình bình hành

\(a,\widehat{AHD}=\widehat{AED}=\widehat{HAE}=90^0\\ \Rightarrow AHDE\text{ là hcn}\\ b,\text{Vì }D\text{ là trung điểm }BC;DE\text{//}AB\left(\perp AC\right)\\ \Rightarrow E\text{ là trung điểm }AC\\ \text{Mà }E\text{ là trung điểm }DM\\ \Rightarrow ADCM\text{ là hbh}\)
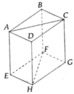
a) Các đường thẳng vuông góc với BF là: AB, BC, CD, DA, AC, EF, FG, GH, HE và FH.
b) (ABCD) và (BCGF), (CDHG) và (EFGH), (ADHE) và (ABCD)
Lưu ý: HS có thể liệt kê tên các cặp mặt phẳng khác.