Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
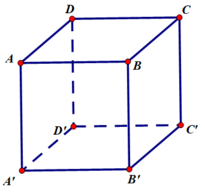
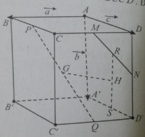
Coi \(ABCD\) là mặt đáy.
Trên tia đối của tia $BA$ lấy $T$ sao cho $BT=BA$. Khi đó:
\(\overrightarrow {AB}=\overrightarrow{BT}; \overrightarrow{CT}=\overrightarrow{DB}\)
Ta có:
\(\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{a}-\overrightarrow{b})\)
\(\Leftrightarrow 2\overrightarrow{OM}=\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{BT}-\overrightarrow {BC}\)
\(\Leftrightarrow 2\overrightarrow{OM}=\overrightarrow{CT}=\overrightarrow{DB}\Leftrightarrow \overrightarrow{OM}=\frac{1}{2}\overrightarrow{DB}\)
Lấy $K$ là trung điểm của $BB'$
Vì $O$ là tâm hình hộp nên $O$ là trung điểm $B'D$
\(\Rightarrow OK\parallel BD; OK=\frac{1}{2}BD\)
\(\Rightarrow \overrightarrow{OK}=\frac{1}{2}{DB}\)
Do đó \(K\equiv M\) hay M là trung điểm của $BB'$

Đáp án A đúng, \(\overrightarrow{AM}=\overrightarrow{A'M'}\)

Các vecto có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vecto A B → là D C → , A ' B ' → , A ' C ' →

a,Ta có : \(A^,=T_{\overrightarrow{v}}\left(A\right)\)
\(\Rightarrow\overrightarrow{AA^,}=\overrightarrow{v}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=2\\y+4=-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=3\\y=-5\end{matrix}\right.\)
\(\Rightarrow A^,\left(3;-5\right)\)
Vậy ...