Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khẳng định thứ (III) kia chính xác là gì nhỉ? Chắc chắn 30G là ko hợp lý rồi

1/ \(\overrightarrow{AM}=3\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MG}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MA}+3\overrightarrow{AG}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AM}=3\overrightarrow{AG}\)
Ban tu ket luan
2/ Bạn coi lại đề bài, đẳng thức kia có vấn đề. 2k-1IB??
\(\overrightarrow{IA}+2k-1+\overrightarrow{IB}+k\overrightarrow{IC}+\overrightarrow{ID}=0\)

+ Ta có :
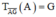
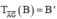 với B’ là điểm thỏa mãn
với B’ là điểm thỏa mãn 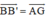
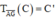 với C’ là điểm thỏa mãn
với C’ là điểm thỏa mãn 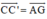
Vậy 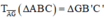 (hình vẽ).
(hình vẽ).
+ 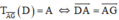 ⇔ D đối xứng với G qua A (hình vẽ).
⇔ D đối xứng với G qua A (hình vẽ).

a: ABCD.A'B'C'D là hình hộp chữ nhật
=>AA'//DD'//BB'//CC'
AA'//CC'
=>AA'//(CC'D'D)
B'B//D'D
=>B'B//(CC'D'D)
mà AA'//(CC'D'D)
và A'A và B'B cùng thuộc mp(AA'B'B)
nên (AA'B'B)//(CC'D'D)
b: Xét tứ giác ADC'B' có
AD//B'C'
AD=B'C'
Do đó: ADC'B' là hình bình hành
=>AB'//DC'
=>AB'//(C'BD)(1)
Xét tứ giác BDD'B' có
BB'//DD'
BB'=D'D
Do đó: BDD'B' là hình bình hành
=>BD//B'D'
=>B'D'//(C'BD)(2)
Từ (1) và (2) suy ra (C'BD)//(AB'D')
c: Gọi G là trọng tâm của ΔABC
Xét ΔBAC có
BO là đường trung tuyến
G là trọng tâm
Do đó: B,O,G thẳng hàng và \(BG=\dfrac{2}{3}BO\)
Gọi M là giao điểm của AG với BC; M' là giao điểm của A'G' với B'C'
Xét ΔABC có
G là trọng tâm
M là giao điểm của AG với BC
Do đó: M là trung điểm của BC và \(AG=\dfrac{2}{3}AM\)
Xét ΔA'B'C' có
G' là trọng tâm
A'G' cắt B'C' tại M'
Do đó: M' là trung điểm của B'C'
Xét ΔABM và ΔA'B'M' có
AB=A'B'
\(\widehat{ABM}=\widehat{A'B'M'}\)
BM=B'M'
Do đó: ΔABM=ΔA'B'M'
=>AM=A'M'
Xét hình thang BCC'B' có
M,M' lần lượt là trung điểm của CB,C'B'
=>MM' là đường trung bình
=>MM'//BB'//CC'
=>MM'//AA'
Xét tứ giác AA'M'M có
MM'//AA'
AM=A'M'
Do đó: AA'M'M là hình bình hành
=>AM//A'M'
=>AG//A'G'
=>A'G'//(ABCD)


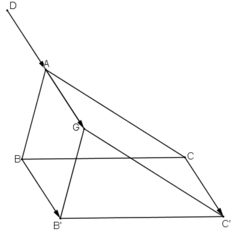
- Dựng hình bình hành ABB'G và ACC'G. Khi đó ta có: \(\overrightarrow{AG}=\overrightarrow{BB'}=\overrightarrow{CC'}\)
. Suy ra \(^T\overrightarrow{AG}\left(A\right)=G,^T\overrightarrow{AG}\left(B\right)=B',^T\overrightarrow{AG}\left(C\right)=C'\)
Do đó ảnh của tam giác ABC qua phép tịnh tiến theo vectơ \(\overrightarrow{AG}\) là tam giác GB'C'.
- Trên tia GA lấy điểm D sao cho A là trung điểm của GD. Khi đó ta có \(\overrightarrow{DA}=\overrightarrow{AG}\). Do đó, \(^T\overrightarrow{AG}\left(D\right)=A\).

- Dựng hình bình hành ABB'G và ACC'G. Khi đó ta có: −−→AG=−−→BB′=−−→CC′AG→=BB′→=CC′→
. Suy ra T−−→AG(A)=G,T−−→AG(B)=B′,T−−→AG(C)=C′TAG→(A)=G,TAG→(B)=B′,TAG→(C)=C′
Do đó ảnh của tam giác ABC qua phép tịnh tiến theo vectơ −−→AGAG→ là tam giác GB'C'.
- Trên tia GA lấy điểm D sao cho A là trung điểm của GD. Khi đó ta có −−→DA=−−→AGDA→=AG→. Do đó, T−−→AG(D)=ATAG→(D)=A.

Lời giải:
Coi \(ABCD\) là mặt đáy.
Trên tia đối của tia $BA$ lấy $T$ sao cho $BT=BA$. Khi đó:
\(\overrightarrow {AB}=\overrightarrow{BT}; \overrightarrow{CT}=\overrightarrow{DB}\)
Ta có:
\(\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{a}-\overrightarrow{b})\)
\(\Leftrightarrow 2\overrightarrow{OM}=\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{BT}-\overrightarrow {BC}\)
\(\Leftrightarrow 2\overrightarrow{OM}=\overrightarrow{CT}=\overrightarrow{DB}\Leftrightarrow \overrightarrow{OM}=\frac{1}{2}\overrightarrow{DB}\)
Lấy $K$ là trung điểm của $BB'$
Vì $O$ là tâm hình hộp nên $O$ là trung điểm $B'D$
\(\Rightarrow OK\parallel BD; OK=\frac{1}{2}BD\)
\(\Rightarrow \overrightarrow{OK}=\frac{1}{2}{DB}\)
Do đó \(K\equiv M\) hay M là trung điểm của $BB'$
Please, ai giúp mk câu b,c,d với ạ 🥺🥺🥺