Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác MNIH có
MH//NI
MN//IH
góc MHI=90 độ
Do đó: MNIH là hình chữ nhật
b: Xét ΔMHQ vuông tại H và ΔNIP vuông tại I có
MQ=NP
góc Q=góc P
Do đó: ΔMHQ=ΔNIP
=>QH=IP
c: Xét ΔMKQ có
MH vừa là đường cao, vừa là trung tuyến
nên ΔMKQ cân tại M
=>góc MQK=góc MKQ=góc P
=>MK//NP
mà MN//KP
nên MNPK là hình bình hành
=>MP cắt NK tại trung điểm của mỗi đường
=>M,E,P thẳng hàng

a: Xet tứ giác MPNQ có
I là trung điểm chung của MN và PQ
nên MPNQ là hình bình hành
b:M đối xứng K qua PQ
nên MK vuông góc với PQ tại trung điểm của MK
=>H là trung điểm của MK
Xét ΔMKN có MH/MK=MI/MN
nên HI//KN
=>KN vuông góc với KM
c: M đối xứng K qua PQ
nên QM=QK
=>QK=PN
Xét tứ giác PQNK có
PQ//NK
PN=QK
Do đó: PQNK là hình thang cân

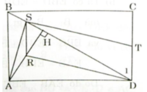
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)
⇒ ΔAHD ∼ ΔDCB (g.g)
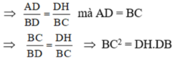
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB
⇒ ∠HSR = ∠HBA (đồng vị)
Mà ∠HBA = ∠D1
⇒ HSR = ∠D1
Do đó ΔSHR ∼ ΔDCB (g.g)
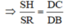
![]()
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2
mà AB = CD và AB // CD (gt)
⇒ SR // DT và SR = DT
Do đó Tứ giác DRST là hình bình hành
d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o
a: Xét ΔNMH vuông tại H và ΔNQM vuông tại M có
góc MNH chung
=>ΔNMH đồng dạng với ΔNQM
b: ΔNMH đồng dạng với ΔNQM
=>NH/NM=NM/NQ
=>NM^2=NH*NQ=PQ^2
c: Gọi A là trung điểm của HM
Xét ΔHMN có HK/HN=HA/HM=1/2
nên AK//MN và AK=1/2MN
=>AK//QI và AK=QI
=>AKIQ là hình bình hành
=>KA//QI
=>KA vuông góc MQ
Xét ΔMQK có
KA,MH là đường cao
KA cắt MH tại A
=>A là trực tâm
=>QA vuông góc MK
=>KI vuông góc KM
=>góc MKI=90 độ