Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)
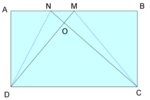
Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)

Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
AB=a ; BC=b
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC

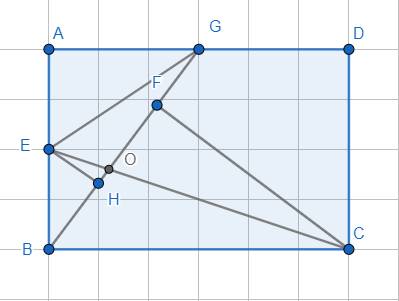
Kẻ \(EH\perp BG\), \(CF\perp BG\)
Ta có: \(S_{ABD}=S_{GBC}=\dfrac{1}{2}.AB.AD=\dfrac{1}{2}.S_{ABCD}\)
\(S_{BAG}=\dfrac{1}{2}.AB.AG=\dfrac{1}{2}.AB.\dfrac{1}{2}AD=\dfrac{1}{4}.AB.AD=\dfrac{1}{2}S_{ABD}\)
\(S_{GEB}=\dfrac{1}{2}.AG.EB=\dfrac{1}{2}.AG.\dfrac{1}{2}.AB=\dfrac{1}{4}.AG.AB=\dfrac{1}{2}S_{ABG}\)
\(\Rightarrow S_{GEB}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}S_{ABCD}=\dfrac{1}{8}S_{ABCD}=\dfrac{1}{4}S_{GBC}\)
\(\Leftrightarrow\dfrac{1}{2}.EH.BG=\dfrac{1}{4}.\dfrac{1}{2}CF.BG\)
\(\Leftrightarrow EH=\dfrac{1}{4}CF\)
Lại có: \(S_{OBE}=\dfrac{1}{2}OB.EH=\dfrac{1}{2}OB.\dfrac{1}{4}CF=\dfrac{1}{4}S_{OBC}\)
Ta có: \(S_{CBE}=S_{OBE}+S_{OBC}=S_{OBE}+4S_{OBE}=5S_{OBE}\)
\(S_{CBE}=5.10=50\left(cm^2\right)\)
Mà \(S_{CBE}=\dfrac{1}{2}S_{CBA}=\dfrac{1}{4}S_{ABCD}\Rightarrow S_{ABCD}=200\left(cm^2\right)\)

Giải thích các bước giải:
a) Xét tam giác ABC và AMC có chung chiều cao hạ từ đỉnh C mà M là trung điểm AB nên AB = 2 x AM => S_ABC = 2 x S_AMC
Xét tam giác AMC với AMD có chung đáy AM, chiều cao hạ từ đỉnh D đáy AM = chiều cao từ đỉnh C đáy AM => S_AMC = S_AMD.
b) Nối AN và EN
Xét các tam giác AMC và ANC đều = 1/4 diện tích hình bình hành = 15 cm2. Mặt khác 2 tam giác này có chung đáy AC => chiều cao hạ từ đỉnh M xuống đáy AC = chiều cao từ đỉnh N đáy AC.
Xét tam giác ENC và EMC chung đáy EC, chiều cao bằng nhau => S_ENC = S_EMC. (1)
Xét tam giác EDN và ENC chung đỉnh E, đáy DN = NC => S_EDN = S_ENC (2)
Xét S tam giác AMD = S_AMC (phần a đã chứng minh) có chung AME => S_AED = S_EMC (3)
Từ (1) ; (2) và (3) => S_EMC = S_ENC = S_EDN = S_AED.
Ta có S_MBC = 15 cm2 => S_ACD = 15 x 2 = 3 (cm2)
Mà S_ACD = S_ENC + S_EDN + S_AED và 3 tam giác này bằng nhau nên :
S_ENC = 30 : 3 = 10 (cm2) mà S_ENC = S_MEC.
Vậy diện tích MEC = 10 cm2.
c) Từ S_MEC = 10 cm2 => S_MEA = 15 - 10 = 5 (cm2)
Xét có chung chiều cao đỉnh M mà S_MEA/S_MCA = 5/15 = 1/3 =>đáy AE = 1/3 AC
(với cách chứng minh tương tự ta có S_NGC = 5 cm2 và GC = 1/3 AC)
Vậy EG = AC - 1/3 AC - 1/3 AC = 1/3AC
Vậy AE = EG = GC
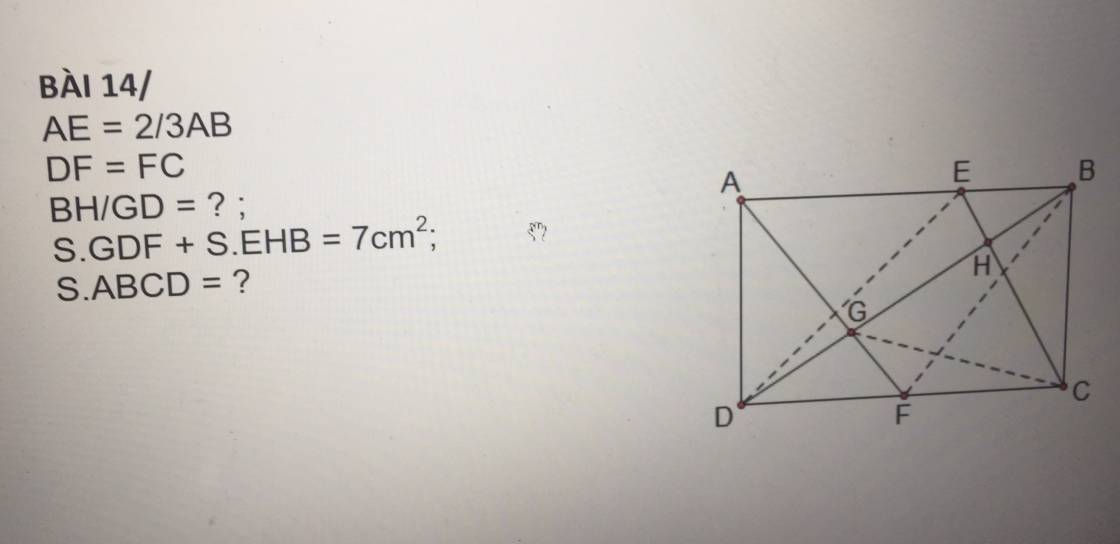
bó tay .com