Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABD vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(AH^2=HB\cdot HD\left(1\right)\)
Ta có: \(\widehat{HDN}=\widehat{HBA}\)
\(\widehat{HMB}=\widehat{HBA}\left(=90^0-\widehat{BAH}\right)\)
Do đó: \(\widehat{HDN}=\widehat{HMB}\)
Xét ΔHDN vuông tại H và ΔHMB vuông tại H có
\(\widehat{HDN}=\widehat{HMB}\)
Do đó: ΔHDN\(\sim\)ΔHMB
Suy ra: \(\dfrac{HD}{HM}=\dfrac{HN}{HB}\)
hay \(HD\cdot HB=HM\cdot HN\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(HA^2=HM\cdot HN\)

a: ΔABD vuông tại A
=>\(BD^2=AB^2+AD^2\)
=>\(BD^2=9^2+12^2=225\)
=>BD=15(cm)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH\cdot BD=AB\cdot AD\)
=>\(AH\cdot15=12\cdot9=108\)
=>AH=108/15=7,2(cm)
XétΔABD vuông tại A có \(sinBDA=\dfrac{AB}{BD}=\dfrac{9}{15}=\dfrac{3}{5}\)
nên \(\widehat{BDA}\simeq37^0\)
b: Xét ΔAHB vuông tại H có HI là đường cao
nên \(AI\cdot AB=AH^2\left(1\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\left(2\right)\)
Từ (1) và (2) suy ra \(AI\cdot AB=HD\cdot HB\)
c: Xét ΔHDN vuông tại H và ΔHMB vuông tại H có
\(\widehat{HDN}=\widehat{HMB}\left(=90^0-\widehat{DBC}\right)\)
Do đó: ΔHDN đồng dạng với ΔHMB
=>HD/HM=HN/HB
=>\(HM\cdot HN=HD\cdot HB=HA^2\)

b: Xét ΔADM vuông tại D có DH là đường cao ứng với cạnh huyền AM
nên \(AH\cdot AM=AD^2\left(1\right)\)
Xét ΔADB vuông tại A có AH là đường cao ứng với cạnh huyền DB
nên \(DH\cdot DB=AD^2\left(2\right)\)
Từ (1) và (2) suy ra \(DH\cdot DB=AH\cdot AM\)

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔADK vuông tại D có DH là đường cao ứng với cạnh huyền AK, ta được:
\(AH\cdot AK=AD^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔADB vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(DH\cdot DB=AD^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AH\cdot AK=DH\cdot DB\)

a: Ta có: AD=BC
mà BC=15cm
nên AD=15cm
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow BD^2=15^2+8^2=289\)
hay BD=17(cm)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABD vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(AH\cdot BD=AB\cdot AD\)
\(\Leftrightarrow AH=\dfrac{8\cdot15}{17}=\dfrac{120}{17}\left(cm\right)\)

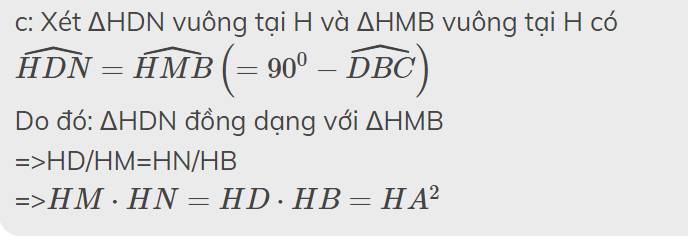

a,Vì ABCD là hình chữ nhật => BC = AD = 15 cm
Xét tam giác ABD vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABD
\(BD^2=AB^2+AD^2=64+225=289\Rightarrow BD=17\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AD^2}\Rightarrow\frac{1}{AH^2}=\frac{1}{64}+\frac{1}{225}=\frac{225+64}{64.225}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{289}{14400}\Leftrightarrow AH^2=\frac{14400}{289}\Leftrightarrow AH=\frac{120}{17}\)
b, Xét tam giác AHB vuông tại H đường cao HI
\(AH^2=IA.AB\)( hệ thức lượng ) (1)
Xét tam giác ABD vuông tại A đường cao AH
\(AH^2=DH.BH\)( hệ thức lượng ) (2)
Từ (1) ; (2) suy ra \(IA.AB=DH.BH\)( đpcm )