Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Phương pháp:
+) Gọi b là độ dài cạnh bên, sử dụng giả thiết diện tích xung quanh gấp đôi diện tích đáy biểu diễn b theo a.
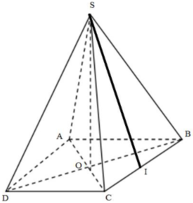
+) Gọi O = AC ∩ BD ⇒ SO ⊥ (ABCD)
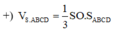
Cách giải:
Gọi b là độ dài cạnh bên, I là trung điểm của BC ⇒ SI ⊥ BC
Tam giác SIB vuông tại I
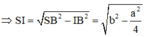
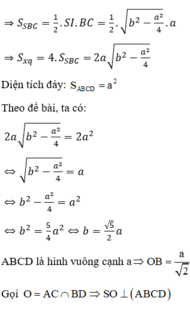
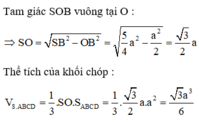

Đáp án là D
Thể tích khối chóp
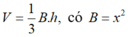
Gọi O là tâm của hình vuông, I là trung điểm DC thì SI ⊥ CD .
Đặt SO = h. Có
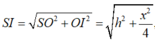
![]()
Suy ra:
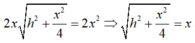
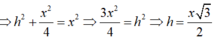
Lúc đó:
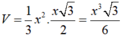

Đáp án A
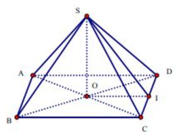
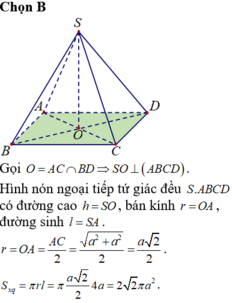
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)


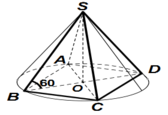
Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên SO ⊥(ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
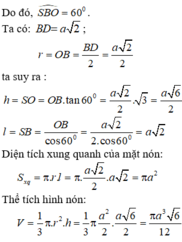

Đáp án A.
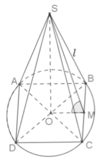
Gọi M là trung điểm của BC, suy ra:
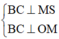
![]()
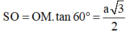
Gọi l, R lần lượt là đường sinh và bán kính của hình nó ngoại tiếp hình chóp, khi đó:
![]()
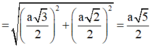
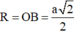
Diện tích xung quanh của hình nón ngoại tiếp hình chóp là:
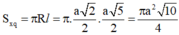
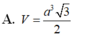
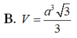
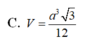
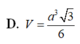
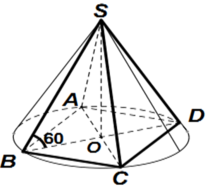
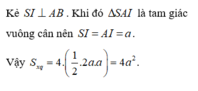
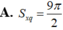
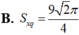
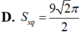
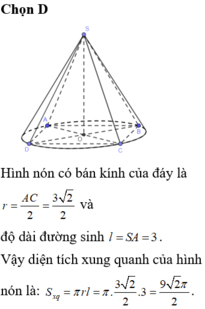
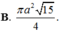
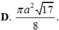
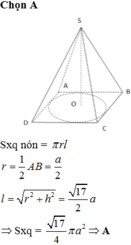
Đáp án D