Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
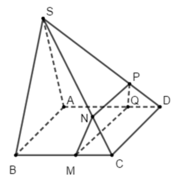
Ta có: MN // BS ⇒ C M C B = C N C S
MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A
NP // CD ⇒ C N C S = D P D S
Do đó: D P D S = D Q D A PQ // SA (Định lý Ta - lét trong tam giác SAD)
Lại có MN // BS và SB ∩ SA = S
Do đó MN không thể song song với PQ
Xét tứ giác MNPQ có NP // MQ (//CD)
Do đó MNPQ là hình thang.
Vậy khẳng địn (1) và (3) đúng.
Đáp án B

Tham khảo hình vẽ:
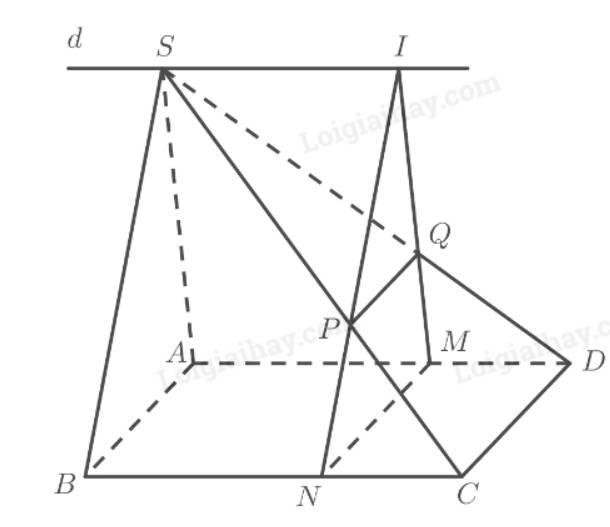
a) Ta có:
\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {SC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\PQ = \left( \alpha \right) \cap \left( {SC{\rm{D}}} \right)\\MN\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel C{\rm{D}}\parallel PQ\).
\( \Rightarrow MNPQ\) là hình bình hành.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in MQ \Rightarrow I \in \left( {SA{\rm{D}}} \right)\\I \in NP \Rightarrow I \in \left( {SBC} \right)\end{array} \right\} \Rightarrow I \in \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\ \Rightarrow SI = \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(A{\rm{D}}\parallel BC\parallel SI\).
Vậy \(I\) luôn luôn thuộc đường thẳng \(d\) đi qua \(S\) song song với \(AD\) và \(BC\) cố định khi \(M\) di động trên \(AD\).

a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD
Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Gọi E là trung điểm của AB
G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)
N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)
Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)

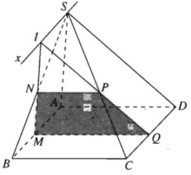
a) Vì M ∈ (SAB)
Và 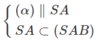 nên (α) ∩ (SAB) = MN
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và 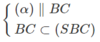 nên (α) ∩ (SBC) = NP
nên (α) ∩ (SBC) = NP
và NP // BC (1)
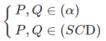 ⇒ (α) ∩ (SCD) = PQ
⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và 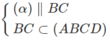 nên (α) ∩ (ABCD) = QM
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
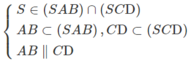 ⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒ 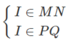
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.


Đáp án A
Gọi F, G, H, I lần lượt là trung điểm của AB; BC; CD và DA
Vì M, N, P, Q lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA.
Do đó ta có: S M S F = S N S G = S P S H = S Q S I = 2 3
Khi đó: MN // FG; NP // GH; QP // IH; MQ // FI
Xét tam giác ABD có FI là đường trung bình (vì F và I lần lượt là trung điểm của AB và AD)
Suy ra FI // BD
Chứng minh tương tự ta có: GH // BD
Nên FI // GH // BD
Tương tự FG // IH // AC
Do đó MQ // NP // FI // GH và MN // PQ // FG // IH
Vậy tứ giác MNPQ là hình bình hành.
Chọn đáp án A