Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Đưa khoảng cách từ M đến (SAC) về khoảng cách từ H đến (SAC).
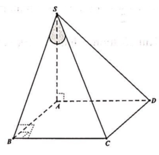
Cách giải: Gọi H là trung điểm của AB ta có SH ⊥ (ABCD)
Ta có (SC;(ABCD)) = (SC;HC) = Góc SCH = 45 0
=>∆SHC vuông cân tại H => 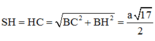
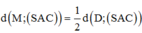
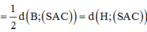
Trong (ABD) kẻ HI ⊥ AC,trong (SHI) kẻ HK ⊥ SI ta có:
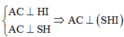
![]()
![]()
Ta có ∆AHI: ∆A CB(g.g) => 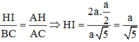
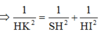
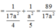
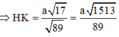

Đáp án B
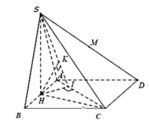
Dễ thấy: S C H ^ = 45 ∘ Gọi H là trung điểm của AB ta có S H ⊥ A B ⇒ S H ⊥ A B C D .
Ta có: S H = H C = a 17 2 .
Ta có: d = d M , S A C = 1 2 d D , S A C
Mà 1 2 d D , S A C = 1 2 d B , S A C nên d = d H , S A C
Kẻ H I ⊥ A C , H K ⊥ S I ⇒ d H , S A C = H K
Ta có: H I = A B . A D 2 A C = a 5 5
Từ đó suy ra: d = H K = S H . H I S I = a 1513 89 .

Đáp ván A
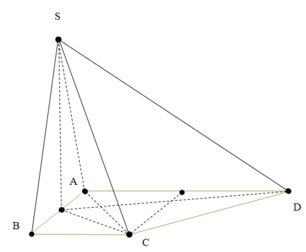
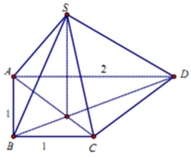
Vì I là hình chiếu của S trên (ABCD)
⇒ ( S C → , ( A B C D ) ) = S C I ⏞
⇒ S I = I C . tan 60 ° = a 5 2 . tan 60 ° = a 15 2
Vậy
V S . I B C = V S . A B C D - V S . A I B - V S . I C D = 1 3 . a 15 2 a + 2 a 2 . a - 1 2 . a 2 . 2 a - 1 2 . a 2 . a = a 3 15 8

Đáp án C
Phương pháp:
- Xác định góc giữa hai đường thẳng: Cho a, b là hai đường thẳng bất kì, đường thẳng a’ // a => (a;b) = (a’;b)
Cách giải:

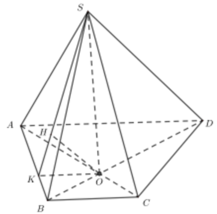
Gọi O, M lần lượt là tâm của hình chữ nhật ABCD và trung điểm của SA
=> MO là đường trung bình của tam giác SAC
=>MO//SC
=>(BD,SC)=(BD,MO)
+) ABCD là hình chữ nhật
![]()
![]()
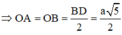
+) M là trung điểm SA
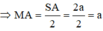
Tam giác MAB vuông tại A
![]()
Tam giác MAO vuông tại A
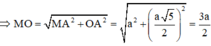
+) Xét tam giác MBO:
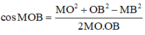

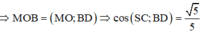
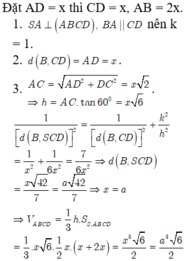



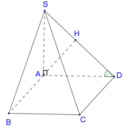

Đáp án C
Ta có
S C , S A B ^ = C S B ^ = 30 ° ⇒ tan 30 ° = B C S B ⇒ S B = 2 a 1 3 = 2 a 3
S A = S B 2 − A B 2 = 2 a 2 − a 2 = a 11
Gọi H là hình chiếu của A lên SD ⇒ A H ⊥ S D C ⇒ A H = d A ; S D C
A H // C D ⇒ A B // S D C ⇒ d A ; S D C = d B ; S D C = A H
Có
1 A H 2 = 1 4 a 2 + 1 11 a 2 = 15 44 a 2 ⇒ A H = a 44 15 = 2 a 11 15