Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
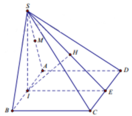
Gọi I, E lần lượt là trung điểm của AB và CD
Vì S M S A = 1 2 ⇒ d M ; S C D = 1 2 d A ; S C A = 1 2 d I ; S C A
= 1 2 I H , trong đó H là hình chiếu của I lên SE
Ta có 1 I H 2 = 1 I S 2 + 1 I E 2 = 1 a 2 − a 2 2 + 1 a 2 = 7 3 a 2
⇒ I H = a 21 7 ⇒ d M ; S C D = 1 2 . a 21 7 = a 21 14

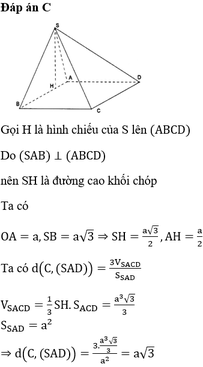
Đáp án C
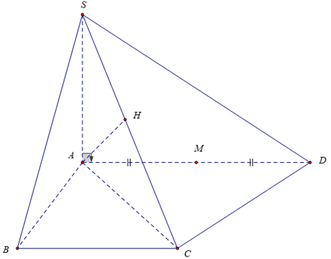
Theo dữ kiện đề bài cho, dễ dàng chứng minh được ΔACD vuông tại cân C và A C = A D 2 = a 2 .
C D ⊥ A C C D ⊥ S A ⇒ C D ⊥ S A C ⇒ S A C ⊥ S C D
Mà S A C ∩ S C D = S C , từ A kẻ A H ⊥ S C . Khi đó d A ; S C D = A H .
Tam giác SAC vuông tại
A: 1 A H 2 = 1 S A 2 + 1 A C 2 = 1 a 2 + 1 2 a 2 = 3 2 a 2 ⇒ d A ; S C D = A H = a 2 3
Mặt khác: A D ∩ S C D = D và M là trung điểm AD nên:
d M ; S C D d A ; S C D = M D A D = 1 2 ⇒ d M ; S C D = 1 2 d A ; S C D = a 6 6

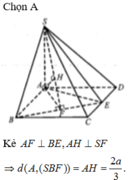
Đáp án là D
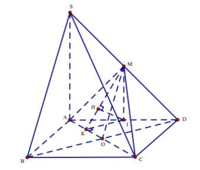
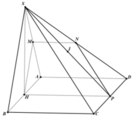
+ Gọi O là giao điểm của AC,BD
⇒ MO \\ SB ⇒ SB \\ ACM
⇒ d SB,ACM = d B,ACM = d D,ACM .
+ Gọi I là trung điểm của AD ,
M I \ \ S A ⇒ M I ⊥ A B C D d D , A C M = 2 d I , A C M .
+ Trong ABCD: IK ⊥ AC (với K ∈ AC ).
+ Trong MIK: IH ⊥ MK (với H ∈ MK ) (1) .
+ Ta có: AC ⊥ MI ,AC ⊥ IK ⇒ AC ⊥ MIK
⇒ AC ⊥ IH (2) .
Từ 1 và 2 suy ra
IH ⊥ ACM ⇒ d I ,ACM = IH .
+ Tính IH ?
- Trong tam giác vuông MIK. : I H = I M . I K I M 2 + I K 2 .
- Mặt khác: M I = S A 2 = a , I K = O D 2 = B D 4 = a 2 4
⇒ I H = a a 2 4 a 2 + a 2 8 = a 3
Vậy d S B , A C M = 2 a 3 .
Lời giải khác
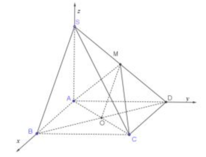


Đáp án B.
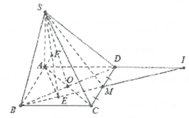
Gọi I là trung điểm của SP. Theo định lý Talet:
d 1 H M N = 1 2 d S H M N . Ta cần tính d S H M N .
Bước 1: Tìm V S . H M N
Ta có:
V S . H M N V S . H A D = 1 2 . 1 2 = 1 4 ; V S . H A D V S . A B C D = 1 4
Giả sử a = 1
Dễ thấy
V S . A B C D = 1 3 S H . S A B C D = 1 3 . 3 2 . 3 2 = 1 4
⇒
V
S
.
H
M
N
=
1
16
.
1
4
=
1
64
.
Bước 2: Tìm S H M N . Ta có: M H → = − 1 2 B S → và M N → = 1 2 B C → ⇒ H M N = 180 ° − S B C .
Do đó
sin H M N = sin S B C ⇒ S H M N = 1 2 M H . M N . sin H M N = 1 4 . S S B C .
Tam giác SBC có SB = BC = 1;
S C = S H 2 + H C 2 = 2 S H = 6 2 ⇒ S S B C = 15 8 .
Do đó S H M N = 1 4 . 15 8 = 15 32 .
Bước 3: Sử dụng công thức:
d S H M N = 3. V S . H M N S H M N = 3 64 . 32 15 = 15 10 ⇒ d I H M N = 1 2 . 15 10 = 15 20 .


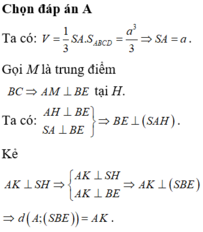

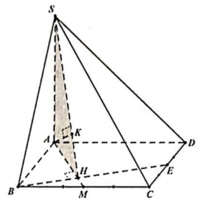
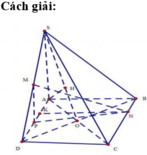

Đáp án B
d M ; S A B = d D , S A B = D A = a