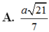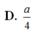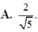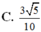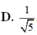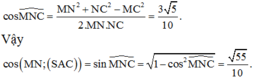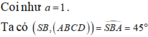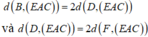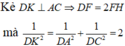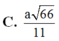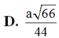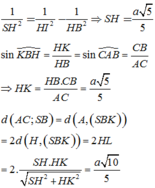Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
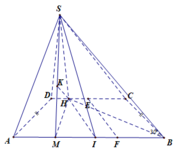
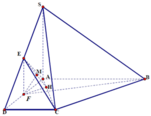
Gọi M, E là trung điểm của AI và CD
Kẻ S H ⊥ C D do mặt phẳng (SCD) vuông góc với mặt phẳng
(ABCD) nên S H ⊥ ( A B C D ) . Mặt khác SA=SI
⇒ S M ⊥ A I ⇒ A I ⊥ ( S H M ) ⇒ H K ⊥ ( S A I ) mà CD
Song song với (SAB) ⇒ H K là khoảng cách cần tìm.
Qua E kẻ đường thẳng song song với BC cắt AB tại F
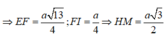
⇒ H B = a 3 ; S H = H B . tan 30 o = a 3 . 1 3 = a
Ta có 1 H K 2 = 1 S H 2 + 1 H M 2 = 1 a 2 + 4 3 a 2 = 7 3 a 2
⇒ H K = a 21 7

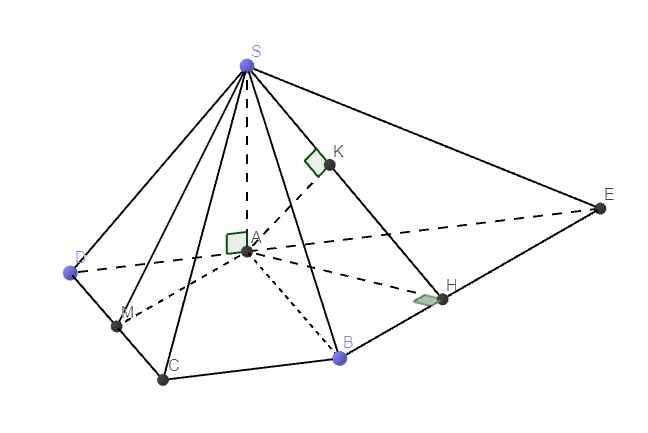
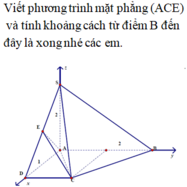
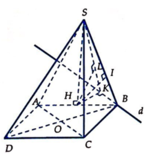
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
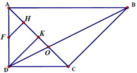
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)

Chọn đáp án C
HC là hình chiếu của SC lên mặt phẳng (ABCD).
Góc giữa SC với mặt phẳng (ABCD) là: S C H ^ = 45 °
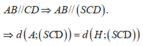
Kẻ 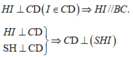
Kẻ 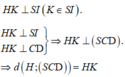
Ta có: ![]()
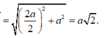
Tam giác SHC vuông cân tại H vì ![]()
Mặt khác: HI = AD = a
Xét tam giác SHI vuông tại H: 
![]()
![]()