Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi K là giao điểm của AB và CD
\(K\in AB\subset\left(SAB\right)\)
\(K\in CD\subset\left(SCD\right)\)
Do đó: \(K\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SK\)
b: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
c: Chọn mp(SCD) có chứa CD
\(N\in SC\subset\left(SCD\right)\)
\(P\in SD\subset\left(SCD\right)\)
Do đó: \(NP\subset\left(SCD\right)\)
mà \(NP\subset\left(MNP\right)\)
nên (SCD) giao (MNP)=NP
Gọi E là giao điểm của CD với NP
=>E là giao điểm của CD với (MNP)
Chọn mp(SBD) có chứa MP
\(BD\subset\left(SBD\right)\)
\(BD\subset\left(ABCD\right)\)
Do đó: \(BD\subset\left(SBD\right)\cap\left(ABCD\right)\)
Gọi F là giao điểm của MP với BD
=>F là giao điểm của MP với (ABCD)

a: Ta có: CD//AB
AB\(\subset\)(SAB)
CD không nằm trong mp(SAB)
Do đó: CD//(SAB)
b: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình của ΔSBD
=>MN//BD
Xét (CMN) và (ABCD) có
\(C\in\left(CMN\right)\cap\left(ABCD\right)\)
MN//BD
Do đó: (CMN) giao (ABCD)=xy, xy đi qua C và xy//MN//BD

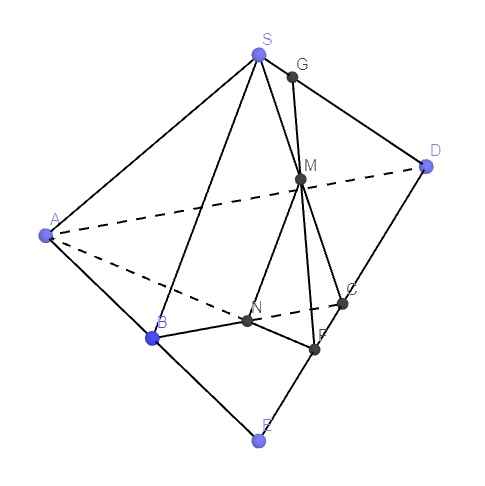
a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6)

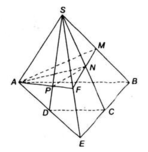
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
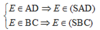
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.

1.
Gọi \(O=AC\cap BD\)
\(AM\in\left(SAC\right)\)
Mà \(\left(SAC\right)\cap\left(SBD\right)=SO\)
\(\Rightarrow J=AM\cap SO\)
Qua M kẻ \(d//AB\Rightarrow N=d\cap SD\)

Gọi E là giao điểm AB và CD
\(\Rightarrow E=\left(SAB\right)\cap\left(SCD\right)\)
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
b.
Do M là trung điểm SC, N là trung điểm BC
\(\Rightarrow MN\) là đường trung bình tam giác SBC
\(\Rightarrow MN||SB\)
Mà \(SB\in\left(SBD\right)\Rightarrow MN||\left(SBD\right)\)
c.
Trong mp (ABCD), nối AN cắt CD kéo dài tại F
Trong mp (SCD), nối FM kéo dài cắt SD tại G
\(\Rightarrow G=SD\cap\left(AMN\right)\)