Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp:
- Dựng mặt phẳng chứa SO và song song với AB .
- Sử dụng lý thuyết: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường thẳng này đến mặt phẳng song song với nó và chứa đường thẳng kia.
- Đưa bài toán về tính khoảng cách từ điểm đến mặt phẳng và kết luận
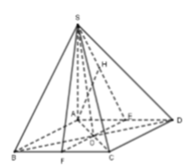

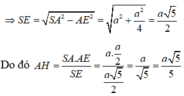

Đáp án D.
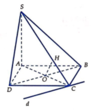
Trong mp A B C D gọi O là giao điểm của AC và BD.
Trong mặt phẳng S A C , qua O kẻ đường thẳng vuông góc với SC, cắt SC tại H.
Ta có B D ⊥ A C B D ⊥ S A ⇒ B D ⊥ S A C ⇒ B D ⊥ O H ⇒ O H là đường vuông góc chung của hai đường thẳng SC và BD.
Lại có A C = a 2 ⇒ C S = S A 2 + A C 2 = a 2 + 2 a 2 = 3 a 2 = a 3 .
Hai tam giác COH và CSA đồng dạng với nhau. Suy ra
O H S A = C O C S ⇒ O H = S A . C O C S = a . a 2 2 a 3 = a 6 6
Vậy khoảng cách giữa hai đường thẳng SC và BD bằng a 6 6 .
Chọn đáp án D.

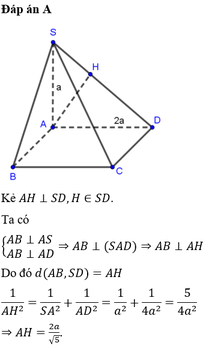
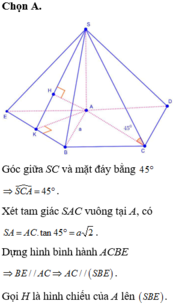

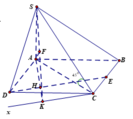


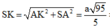
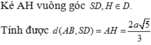


Gọi E, F lần lượt là trung điểm của AD, BC thì AB / / EF ⇒ AB / / (SEF)
Mà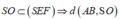
Dựng A H ⊥ S E
Ta thấy: FE / / AB, A B ⊥ ( S A D ) ⇒ F E ⊥ ( S A D ) ⇒ F E ⊥ A H
Mà A H ⊥ S E nên A H ⊥ ( S E F ) ⇔ d ( A , ( S E F ) ) = A H
ABCD là hình vuông cạnh a nên B D = a 2
Dễ dàng chứng minh được ∆ S A B = ∆ S A D c . g . c ⇒ S B = S D
Tam giác SBD cân có S B D = 60 ° nên đều ⇒ S D = B D = a 2
Tam giác SAD vuông tại A có S A = S D 2 - A D 2 = 2 a 2 - a 2 = a
Tam giác SAE vuông tại A có
Do đó
Chọn đáp án D.