Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

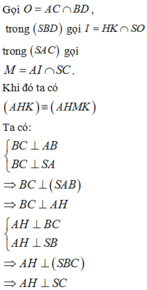
Hoàn toàn tương tự ta chứng minh được
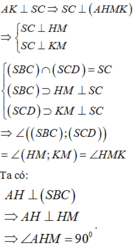
Tương tự ta có
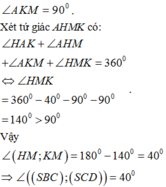
Chọn A.

Đáp án B.
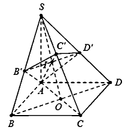
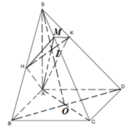
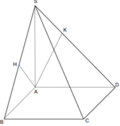
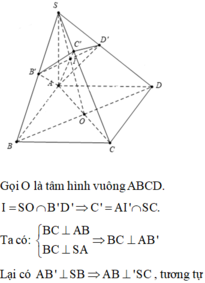
Gọi O là tâm của hình vuông ABCD, nối S O ∩ B ' D ' = I .
Và nối AI cát SC tại C’ suy ra mp (AB’D’) cắt SC tại C’.
Tam giác SAC vuông tại A, có S C 2 = S A 2 + A C 2 = 6 a 2 ⇒ S C = a 6 .
Ta có B C ⊥ S A B ⇒ B C ⊥ A B ' và S B ⊥ A B ' ⇒ A B ' ⊥ S C .
Tương tự A D ' ⊥ S C suy ra S C ⊥ ( A B ' D ' ) ≡ ( A B ' C ' D ' ) ⇒ S C ⊥ A C ' .
Mà S C ' . S C = S A 2 ⇒ S C ' S C = S A 2 S C 2 = 2 3 và S B ' S B = S A 2 S B 2 = 4 5 .
Do đó V S . A B ' C ' = 8 15 V S . A B C = 8 30 V S . A B C D mà V S . A B C D = 1 3 . S A . S A B C D = 2 a 3 3 .
Vậy thể tích cần tính là V S . A B ' C ' D ' = 2 . V S . A B ' C ' = 16 a 3 45
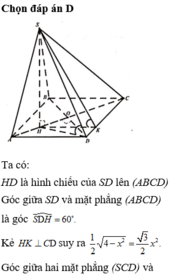



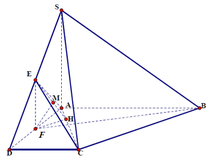
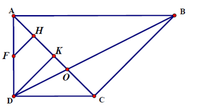

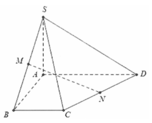


Ta có A E = B C A E / / B C suy ra AECB là hình bình hành. Do A B C ^ = 90 0 nên AECB là hình chữ nhật.
Suy ra C E ⊥ A D mà S A ⊥ C E ⇒ C E ⊥ S A D ⇒ C E ⊥ S D .
Ta lại có E K ⊥ S D ⇒ S D ⊥ E K M ⇒ S D ⊥ C K .
Suy ra góc giữa hai mặt phẳng (SAD) và (SCD) là góc EKC