Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Sử dụng công thức ![]()
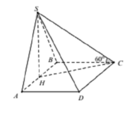
Cách giải: ![]()
Ta có ![]()
Xét tam giác vuông SHC có ![]()
Ta có:
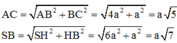
Ta có:
![]()
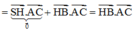
![]()
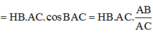
![]()
Lại có ![]()

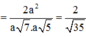

Đáp án C
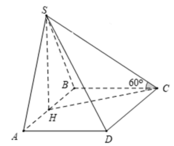
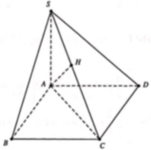
Ta có: H C = B H 2 + B C 2 = a 2
S H = H C . tan S C H = a 2 . tan 60 ∘ = a 6 A C = B A 2 + B C 2 = a 5 , S B = S H 2 + H B 2 = a 7
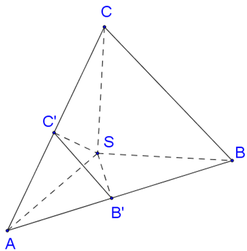
Ta có: S B → . A C → = S H → + H B → . A C → = H B . A C . cos B A C
⇔ S B → . A C → = H B . A C . A B A C = 2 a 2 S B . A C = a 7 . a 5 = a 2 35 ⇒ c os S B , A C = S B → . A C → S B . A C = 2 a 2 a 2 35 ⇒ S B , A C = 70 o 14 ' 28 , 22 ' '

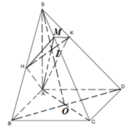
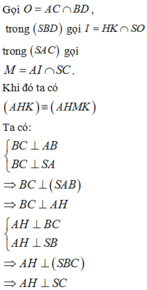
Hoàn toàn tương tự ta chứng minh được
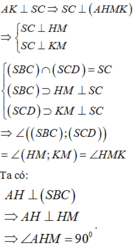
Tương tự ta có
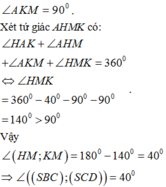
Chọn A.

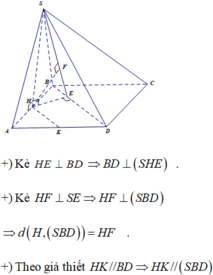
Đáp án B
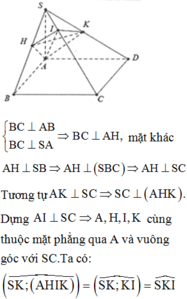
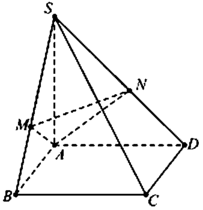
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .

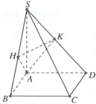
Đáp án C.
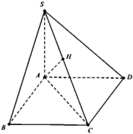
Do:
S C ; A B C ^ = 60 0 ⇒ S C A ^ = 60 0 ⇒ S A = A C tan 60 0 = a 6
Ta có: Δ S A C vuông tại A có đường cao AH.
Khi đó:
S A 2 = S H . S C ⇒ S A 2 S C 2 = S H S C = 6 a 2 6 a 2 + 2 a 2 = 3 4 ⇒ H C S C = 1 4 .
Do đó:
d H ; A B C D = 1 4 d C ; A B C D ⇒ V H . A B C D = 3 4 V S . A B C D = 1 4 . 1 3 . a 6 . 3 a 2 2 = a 2 6 8 .
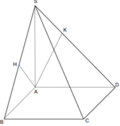


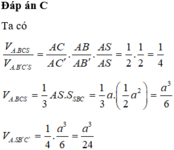
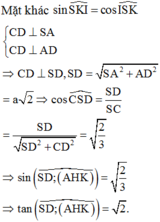

Chọn A.
Phương pháp:
Cách giải: