Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)

Trước hết ta chứng minh 1 bổ đề đơn giản về diện tích tam giác như sau (em tự vẽ hình)
Cho tam giác ABC, trên các cạnh AB và AC lần lượt lấy 2 điểm B' và C', khi đó ta có:
\(\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{AB'.AC'}{AB.AC}\)
Chứng mình: từ C và C' lần lượt hạ CH và C'H' vuông góc AB, khi đó CH song song C'H' nên theo Talet:
\(\dfrac{C'H'}{CH}=\dfrac{AC'}{AC}\)
\(\Rightarrow\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{\dfrac{1}{2}C'H'.AB'}{\dfrac{1}{2}CH.AB}=\dfrac{AC'.AB'}{AC.AB}\)
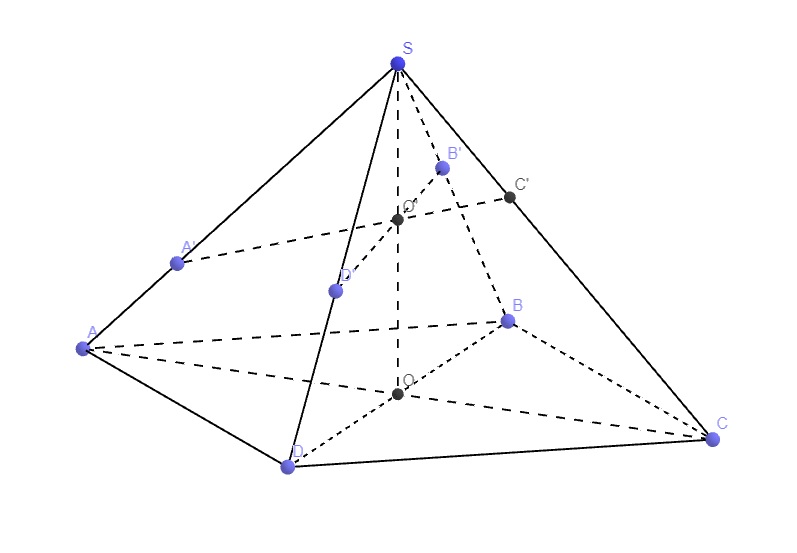
Quay lại bài, gọi O là tâm đáy
Trong mp (SAC), tại O' là giao điểm của SO và A'C'
Ba mặt phẳng (SAC), (SBD), \(\left(\alpha\right)\) cắt nhau theo 3 giao tuyến phân biệt là SO, A'C', B'D' nên 3 giao tuyến này song song hoặc đồng quy.
Mà SO và A'C' cắt nhau tại O' nên 3 đường thẳng nói trên đồng quy tại O'
Ta có:
\(S_{SA'C'}=S_{SA'O'}+S_{SC'O'}\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{S_{SAC}}+\dfrac{S_{SC'O'}}{S_{SAC}}\)
\(\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{2S_{SAO}}+\dfrac{S_{SC'O'}}{S_{SCO}}\Rightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SA'.SO'}{2SA.SO}+\dfrac{SC'.SO'}{2SC.SO}\)
\(\Leftrightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SO'}{2SO}\left(\dfrac{SA'}{SA}+\dfrac{SC'}{SC}\right)\)
\(\Leftrightarrow SA'.SC'=\dfrac{SO'}{2SO}\left(SC.SA'+SA.SC'\right)\)
\(\Leftrightarrow1=\dfrac{SO'}{2SO}\left(\dfrac{SC}{SC'}+\dfrac{SA}{SA'}\right)\)
\(\Leftrightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}=\dfrac{2SO}{SO'}\)
Hoàn toàn tương tự, ta cũng có \(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}=\dfrac{2SO}{SO'}\)
\(\Rightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}\right)=0\)

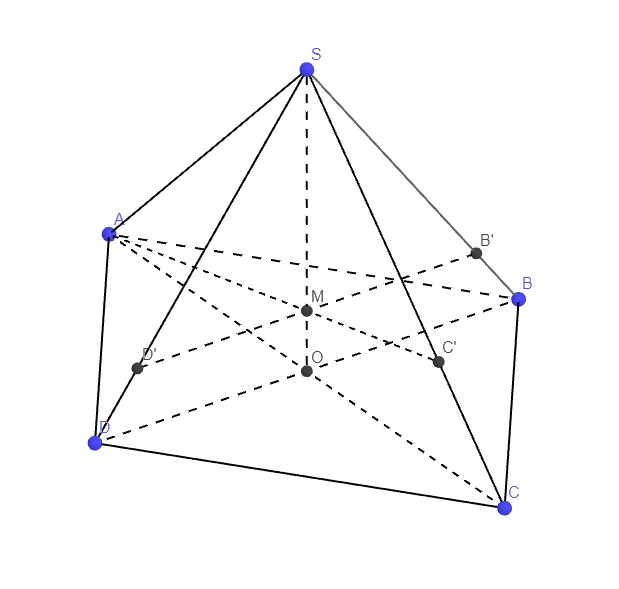
Gọi O là giao điểm AC và BD, theo t/c hình bình hành \(\Rightarrow O\) là trung điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}\\\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\end{matrix}\right.\)
Từ giả thiết:
\(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}+\overrightarrow{MS}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}+\overrightarrow{MO}+\overrightarrow{OS}=\overrightarrow{0}\)
\(\Leftrightarrow5.\overrightarrow{MO}+\overrightarrow{OS}=0\)
\(\Leftrightarrow\overrightarrow{OM}=\dfrac{1}{5}\overrightarrow{OS}\)
Hay M là điểm thuộc đoạn thẳng OS sao cho \(OM=\dfrac{1}{5}OS\) \(\Rightarrow SM=4MO\)
Do M thuộc OS \(\Rightarrow M\in\left(SAC\right)\), kéo dài AM cắt SC tại \(C'\) \(\Rightarrow C'\) là điểm cố định (bất chấp vị trí mặt phẳng (P))
Áp dụng định lý Menelaus trong tam giác SOC với 3 điểm A, M, C' thẳng hàng:
\(\dfrac{MS}{MO}.\dfrac{OA}{AC}.\dfrac{CC'}{C'S}=1\Rightarrow4.\dfrac{1}{2}.\dfrac{CC'}{C'S}=1\Rightarrow\dfrac{CC'}{SC'}=\dfrac{1}{2}\)
Bây giờ tới B' và D'.
Cách đơn giản nhất là đề ko cho biết rõ về mp (P), nó chỉ cần chứa AM là đủ, do đó ta chọn vị trí đơn giản nhất của (P) để tính, đó là (P) song song BD. Khi đó, qua M kẻ đường thẳng song song BD lần lượt cắt SB, SD tại B' và D'
Theo định lý Talet:
\(\dfrac{BB'}{SB'}=\dfrac{DD'}{SD'}=\dfrac{MO}{SM}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{BB'}{SB'}+\dfrac{CC'}{SC'}+\dfrac{DD'}{SD'}=\dfrac{1}{4}+\dfrac{1}{2}+\dfrac{1}{4}=1\)
Trong trường hợp ko muốn làm kiểu chọn mp đặc biệt này thì ta có thể chọn vị trí bất kì cho B', nhưng sẽ tốn thời gian hơn nhiều. Nếu em cần thì cũng có thể giải quyết theo cách ấy.

Bài này ứng dụng 1 phần cách giải của bài này:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24
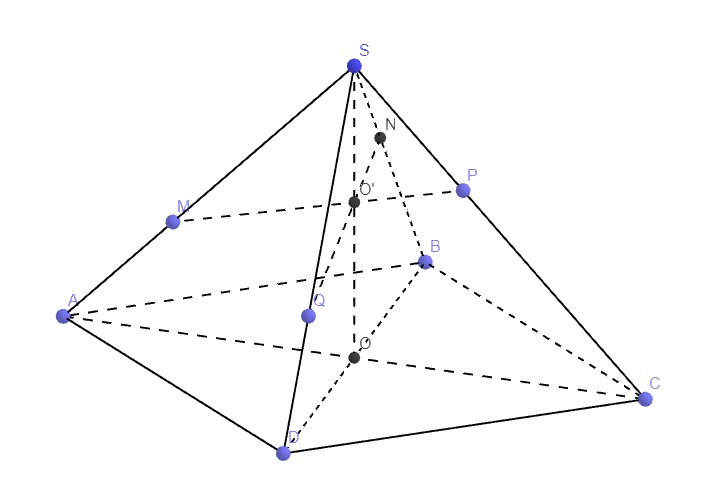
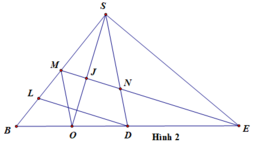
Gọi O' là giao điểm của SO và MP, tương tự như bài trên, ta có 3 đường thẳng SO, MP, NQ đồng quy tại O'
Đồng thời sử dụng diện tích tam giác, ta cũng chứng minh được:
\(3=\dfrac{SA}{SM}+\dfrac{SC}{SP}=\dfrac{2SO}{SO'}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\)
Áp dụng BĐT Cô-si: \(3=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\ge2\sqrt{\dfrac{SB.SD}{SN.SQ}}\Rightarrow SN.SQ\ge\dfrac{4}{9}.SB.SD\)
Theo bổ đề về diện tích tam giác chứng minh ở đầu:
\(\dfrac{S_{SNQ}}{S_{SBD}}=\dfrac{SN.SQ}{SB.SD}\ge\dfrac{\dfrac{4}{9}SB.SD}{SB.SD}=\dfrac{4}{9}\)
\(\Rightarrow S_{SBD}\ge\dfrac{4}{9}.S_{SBD}=\dfrac{4}{9}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{9}\)


Bài này cũng có thể ứng dụng bài này (vẫn là sử dụng diện tích tam giác):
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24
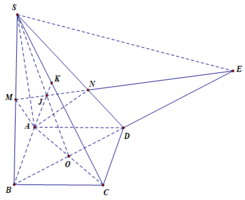
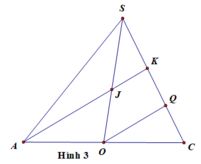
Nhưng đặc biệt hơn 1 chút là nó đi qua điểm A luôn (vậy ta có thể coi như (P) cắt SA tại A và áp dụng nó vẫn đúng):
\(\dfrac{SA}{SA}+\dfrac{SC}{SP}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}=\dfrac{2SO}{SI}=8\)
\(\Rightarrow1+\dfrac{SB}{SN}+\dfrac{SC}{SP}+\dfrac{SD}{SQ}=16\)
\(\Rightarrow\dfrac{SB}{SN}+\dfrac{SC}{SP}+\dfrac{SD}{SQ}=15\)