Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
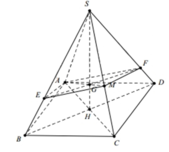
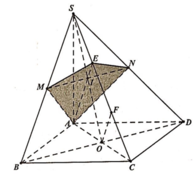
Gọi H là tâm của hình vuông A B C D ; S B H ^ = 60 0 ; H B = a 2 2
Khi đó là trọng tâm tam giác SAC.
Qua G dựng đường thẳng song song với BD cắt SB;SD lần lượt là E và F.
Do tính chất đối xứng ta có:
V S . A E M F V S . A B C D = V S . A E M V S . A B C = S E S B . S M S C = 2 3 . 1 2 = 1 3 .
Mặt khác V A . A B C D = 1 3 S H . S A B C D = 1 3 H B tan 60 0 . a 2 = a 3 6 6 .
Do đó V S . A E M F = 1 3 . a 3 6 6 = a 3 6 18 .

Chọn A
Xét một trường hợp đặc biệt của các điểm M, E, F ta tính được T = 1.

Đáp án D

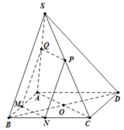
Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I
Qua I kẻ đương thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra S H S B = S K S D = S I S O .
Điểm M ∈ S C thỏa mãn 5 S M = 2 S C ⇒ S M S C = 2 5
Xét tam giác SAC, có:
M S M C . A C A O . I O I S = 1 ⇒ I O S I = 4 3 ⇒ S I S O = 3 7
Khi đó:
V S . A K M V S . A D C = S K S D . S M S C ; V S . A H M V S . A B C = S H S B . S M S C
Suy ra:
V S . A H M K V S . A B C D = S M S C . S H S B = 2 5 . 3 7 = 6 35 ⇒ V S . A H M K = 6 36 V S . A B C D

Đáp án A
Phương pháp giải:
Dùng định lí Thalet và phương pháp tỉ số thể tích để tính thể tích khối chóp cần tìm


Đáp án D
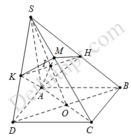
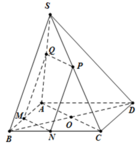
Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I .
Qua I kẻ đường thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra


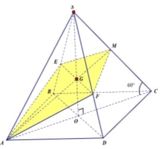

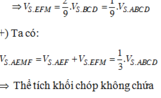

Chọn A
Gọi O là gia điểm của hai đường chéo của hình bình hành ABCD. Gọi I là giao điểm của SO và AM. Khi đó