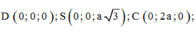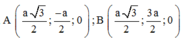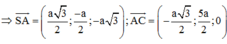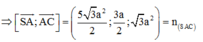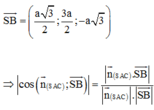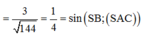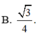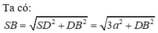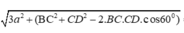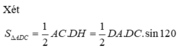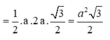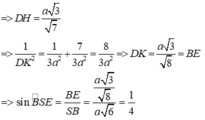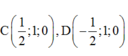Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Hướng dẫn giải:Ta có
![]()
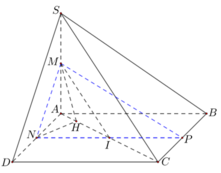
Suy ra tam giác SAD vuông cân tại A nên SA = AD =2a .
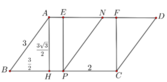
Trong hình thang ABCD , kẻ B H ⊥ A D ( H ∈ A D ) .
Do ABCD là hình thang cân nên A H = A D - B C 2 = a 2 .
Tam giác AHB ,có B H = A B 2 - A H 2 = a 3 2
Diện tích S A B C D = 1 2 ( A D + B C ) . B H = 3 a 3 2 4 .
Vậy V S . A B C D = 1 3 S A B C D . S A = a 3 3 2

Chọn D
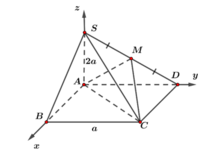
Để thuận tiện trong việc tính toán ta chọn a = 1.
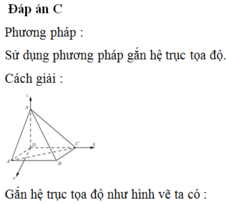
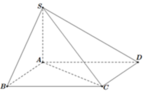
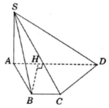
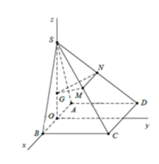
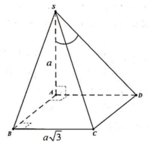
Trong không gian, gắn hệ trục tọa độ Oxyz như hình vẽ sao cho gốc O trùng với điểm A, tia Ox chứa đoạn thẳng AB, tia Oy chứa đoạn thẳng AD, tia Oz chứa đoạn thẳng AS. Khi đó: A(0;0;0), B(1;0;0), C(1;1;0), S(0;0;2), D(0;1;0)
Vì M là trung điểm SD nên tọa độ là M 0 ; 1 2 ; 1
Ta có
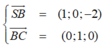
![]()
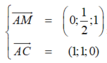
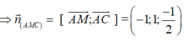
Gọi α là góc giữa hai mặt phẳng (AMC) và (SBC).
Suy ra
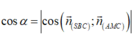
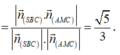
Mặt khác
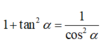
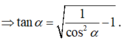
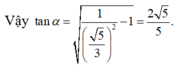

Chọn đáp án C
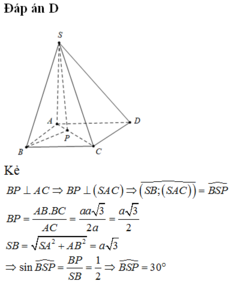
Ta có: 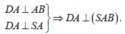
SA là hình chiếu của SD lên mặt phẳng (SAB).
Góc giữa SD với mặt phẳng (SAB) là D S A ^
Ta có: ![]()
Xét tam giác SAD vuông tại A:
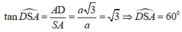

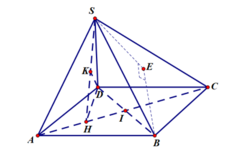
Dễ dàng chứng minh \(BC\perp BD\) (Pitago đảo) \(\Rightarrow BC\perp\left(SBD\right)\)
Đồng thời dễ dàng chứng minh \(AB\perp\left(SAD\right)\)
Từ D kẻ \(DH\perp SA\Rightarrow DH\perp\left(SAB\right)\)
Từ D kẻ \(DK\perp SB\Rightarrow DK\perp\left(SBC\right)\)
\(\Rightarrow\widehat{HDK}\) là góc giữa (SAB) và (SBC)
\(\Rightarrow\widehat{HDK}=30^0\Rightarrow DH=DK.cos30^0=\dfrac{DK\sqrt{3}}{2}\Rightarrow DH^2=\dfrac{3DK^2}{4}\)
Hệ thức lượng: \(\dfrac{1}{DH^2}=\dfrac{1}{SD^2}+\dfrac{1}{AD^2}\Leftrightarrow\dfrac{4}{3DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{a^2}\Rightarrow\dfrac{1}{DK^2}=\dfrac{3}{4SD^2}+\dfrac{3}{4a^2}\) (1)
\(\dfrac{1}{DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{BD^2}=\dfrac{1}{SD^2}+\dfrac{1}{2a^2}\) (2)
(1);(2) \(\Rightarrow\dfrac{3}{4SD^2}+\dfrac{3}{4a^2}=\dfrac{1}{SD^2}+\dfrac{1}{2a^2}\Rightarrow SD=a\)
\(V=\dfrac{1}{3}SD.\dfrac{1}{2}AD\left(AB+CD\right)=...\)