Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

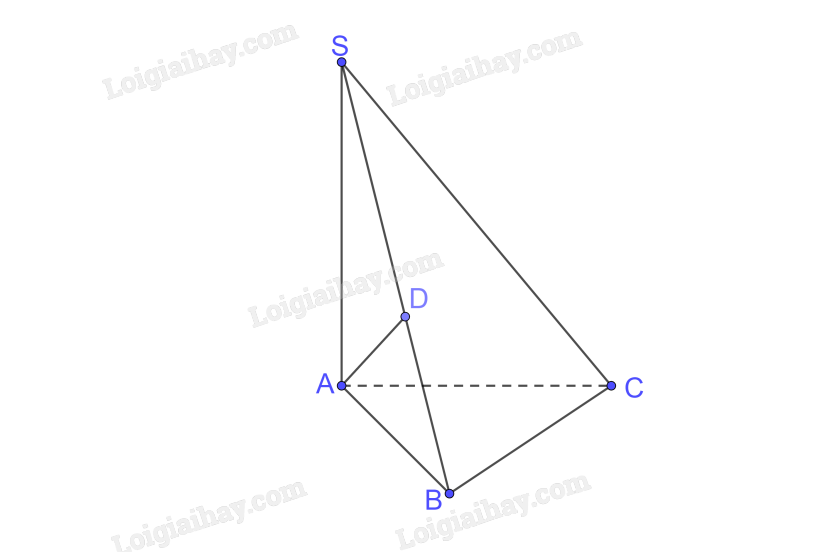
a) Trong (SAB) kẻ \(AD \bot SB\) tại D.
\(\left. \begin{array}{l}BC \bot AD\\SB \bot AD\\BC \cap SB = \left\{ B \right\}\end{array} \right\} \Rightarrow AD \bot \left( {SBC} \right) \Rightarrow \)D là hình chiếu của A trên (SBC).
b) A là hình chiếu của S trên (ABC) \(\left( {SA \bot \left( {ABC} \right)} \right)\)
C là hình chiếu của C trên (ABC)
\( \Rightarrow \) AC là hình chiếu của SC trên (ABC)
\( \Rightarrow \) \(\left( {SC,\left( {ABC} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác SAC vuông tại A có
\(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} \Rightarrow \widehat {SCA} = \arctan \frac{1}{{\sqrt 2 }}\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = \arctan \frac{1}{{\sqrt 2 }}\)

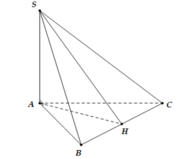
a)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ A là hình chiếu của A trên mặt phẳng (ABC)
\( \Rightarrow \) HA là hình chiếu của SA trên mặt phẳng (ABC)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ B là hình chiếu của B trên mặt phẳng (ABC)
\( \Rightarrow \) HB là hình chiếu của SB trên mặt phẳng (ABC)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ C là hình chiếu của C trên mặt phẳng (ABC)
\( \Rightarrow \) HC là hình chiếu của SC trên mặt phẳng (ABC)
b, Do H là hình chiếu của S trên mặt phẳng (ABC) \( \Rightarrow SH \bot (ABC)\).
Mà \(AB,AC,BC \subset (ABC) \Rightarrow SH \bot AB,SH \bot AC,SH \bot BC\).
Ta có: \(\left\{ \begin{array}{l}SA \bot BC\\SH \bot BC\\SA \cap SH = S\\SA,SH \subset (SAH)\end{array} \right. \Rightarrow BC \bot (SAH) \Rightarrow BC \bot AH\,(1)\)
Tương tự \(\left\{ \begin{array}{l}SC \bot AB\\SH \bot AB\\SC \cap SH = S\\SC,SH \subset (SCH)\end{array} \right. \Rightarrow AB \bot (SCH) \Rightarrow AB \bot CH\,(2)\)
TỪ (1) và (2) \( \Rightarrow \) H là trực tâm của tam giác ABC.
Vì \(\left\{ \begin{array}{l}AB \bot (SCH)\\SC \subset (SCH)\end{array} \right. \Rightarrow AB \bot SC\)

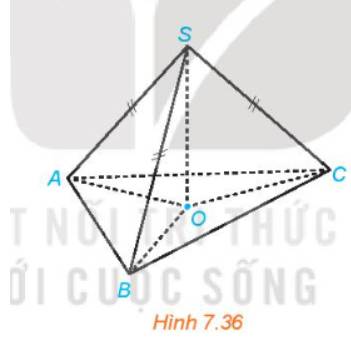
a) O là hình chiếu của S trên mặt phẳng (ABC) nên \(SO \bot \left( {ABC} \right)\)
Mà \(OA,OB,OC \subset \left( {ABC} \right) \Rightarrow SO \bot OA,SO \bot OB,SO \bot OC\)
Xét tam giác SAO vuông tại O \(\left( {SO \bot OA} \right)\) có
\(S{A^2} = O{A^2} + S{O^2}\) (Định lí Pytago)
Xét tam giác SBO vuông tại O \(\left( {SO \bot OB} \right)\) có
\(S{B^2} = O{B^2} + S{O^2}\) (Định lí Pytago)
Xét tam giác SCO vuông tại O \(\left( {SO \bot OC} \right)\) có
\(S{C^2} = O{C^2} + S{O^2}\) (Định lí Pytago)
Mà SA = SB = SC nên OA = OB = OC
Do đó O là tâm đường trọn ngoại tiếp tam giác ABC.
b) O là hình chiếu của S trên mặt phẳng (ABC)
A là hình chiếu của A trên mặt phẳng (ABC)
\( \Rightarrow \) OA là hình chiếu của SA trên mặt phẳng (ABC)
c) \(\left. \begin{array}{l}AO \bot BC\\SO \bot BC\left( {SO \bot \left( {ABC} \right)} \right)\\AO \cap SO = \left\{ O \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAO} \right);SA \subset \left( {SAO} \right) \Rightarrow SA \bot BC\)
d) O là hình chiếu của S trên mặt phẳng (ABC)
A là hình chiếu của A trên mặt phẳng (ABC)
B là hình chiếu của B trên mặt phẳng (ABC)
C là hình chiếu của C trên mặt phẳng (ABC)
\( \Rightarrow \) Tam giác OAB là hình chiếu của tam giác SAB trên mặt phẳng (ABC)
Tam giác OBC là hình chiếu của tam giác SBC trên mặt phẳng (ABC)
Tam giác OCA là hình chiếu của tam giác SCA trên mặt phẳng (ABC)

Đáp án D
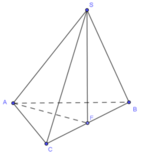
Góc giữa cạnh SA và đáy là S A F ^ ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
![]()
Vậy ![]()

Chọn D.
+) Ta có :
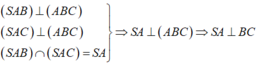
⇒ Suy ra : A đúng.
+) Ta có : 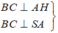
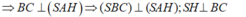
⇒ Suy ra : C đúng.
+) Mặt khác : AH ⊥ CD nên:
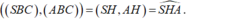
⇒ Suy ra : D sai.
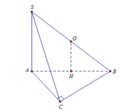

a) Ta có SA \( \bot \) (ABC) nên A là hình chiếu của S trên (ABC)
b) A là hình chiếu của S trên (ABC)
B là hình chiếu của B trên (ABC)
C là hình chiếu của C trên (ABC)
\( \Rightarrow \) Tam giác ABC là hình chiếu của tam giác SBC.
c) B là hình chiếu của C trên (SAB)
S, B là hình chiếu của chính nó trên (SAB)
\( \Rightarrow \) SB là hình chiếu của tam giác SBC trên (SAB)