
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
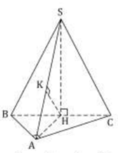

Từ (1), (2) => HK là đoạn vuông góc chung của SA và BC

Tam giác SHA vuông tại A có đường cao HK nên 1 HK 2 = 1 SH 2 + 1 AH 2 = 4 3 a 2 + 4 a 2 = 16 3 a 2 .
⇒ HK = 3 a 4 .

Đáp án A.
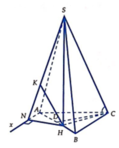
Ta có S C H ^ = 60 ° và
H C = a 7 3 ; S H = H C tan S C H ^ = a 21 3
Từ A kẻ tia A x / / C B (như hình vẽ). Khi đó B C / / S A x và do B A = 3 2 H A nên
d B C , S A = d B C , S A x = d B , S A x = 3 2 d H , S A x
Gọi N và K lần lượt là hình chiếu vuông góc của H trên Ax và SN.
Do A N ⊥ S H N và H K ⊥ S N nên H K ⊥ S A N . Khi đó d B C , S A = 3 2 H K .
Ta có
A H = 2 a 3 ; H N = A H sin N A H ^ = a 3 3 .
Suy ra H K = H N . H S H N 2 + H S 2 = a 42 12 . Vậy d B C , S A = a 42 8 .

Đáp án A
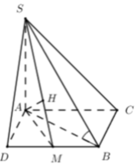
Gọi h là trung điểm của A B ⇒ S H ⊥ A B C D
Kẻ H K ⊥ S A K ∈ S A ⇒ H K ⊥ S A D ⇒ d H ; S A D = H K
Vì A D / / B C ⇒ B C / / m p S A D ⇒ d S A ; B C = d B C ; S A D
= d B ; S A D = 2 × d H ; S A D = 2 H K
Tam giác SAH vuông tại H, có H K = S H . H A S H 2 + H A 2 = a 3 4
Vậy d S A ; B C = 2 H K = 2. a 3 4 = a 3 2

Ta có S A ⊥ A B C ⇒ A B là hình chiếu của SB lên(ABC) .
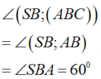
Dựng hình bình hành ACBD.
Ta có
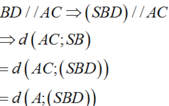
Do tam giác ABC đều

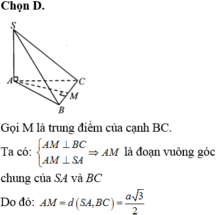
Ta có:
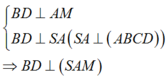
Trong (SAM) kẻ
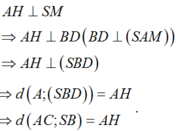
Xét tam giác vuông SAB ta có
![]()
Áp dụng hệ thức lượng trong tam giác vuông SAM ta có:

Chọn A.