K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
23 tháng 3 2017
Chọn D
Phương pháp: Xác định tâm của mặt cầu
ngoại tiếp khối chóp.



CM
29 tháng 11 2018
Đáp án A
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
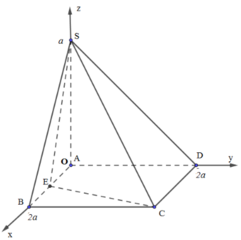
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2
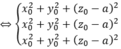
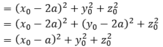
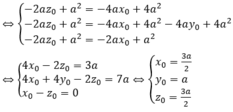
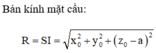
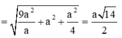
![]()

CM
22 tháng 6 2017
Đáp án C
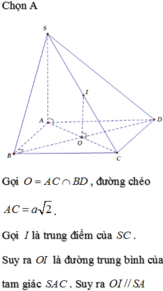
Theo định lí ba đường vuông góc ta có tam giác SBC, SDC lần lượt vuông tại B, D. Gọi I là trung điểm của SC. Từ các tam giác SAC, SBC, SDC vuông ta có:
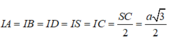
Vậy I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD và bán kính mặt cầu là 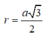
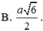
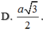

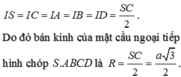
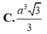
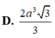
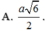
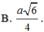
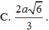
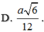
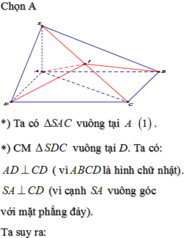

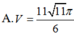
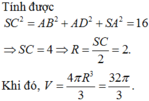

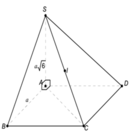



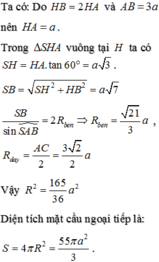
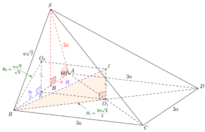

Gọi O là tâm đáy \(\Rightarrow OA=\dfrac{1}{2}AC=\sqrt{2}\)
\(\Rightarrow SO=\sqrt{SA^2-OA^2}=\sqrt{2}\)
\(\Rightarrow OA=OB=OC=OD=SO\Rightarrow\) O đồng thời là tâm mặt cầu ngoại tiếp chóp
\(\Rightarrow R=OA=\sqrt{2}\)
\(\Rightarrow V=\dfrac{4}{3}\pi R^3=\dfrac{8\pi\sqrt{2}}{3}\)