K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

C
3 tháng 5 2017
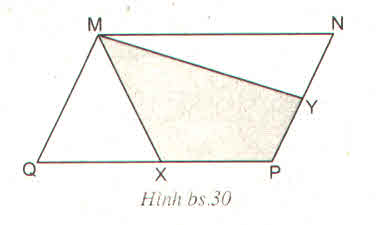
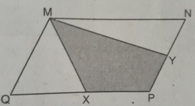
Kẻ đường chéo MP
Ta được SMQX= SMPX
SMNY=SMPY
=> SMXPY= SMPX + SMPY
Khi đó \(S_{MXPY}=\dfrac{1}{2}S\)
Nhớ tick nhé !
DN
3 tháng 5 2017
Sau khi kẻ đường thẳng MP ta có:
\(\Delta MPQ=\Delta MPN\) (cạnh-cạnh-cạnh)
=> \(\dfrac{1}{2}\)SMPQ = \(\dfrac{1}{2}S_{MPN}\)
hay \(\Delta MPX=\Delta MPY\).
Vì \(S_{MPX}+S_{MPY}=S_{MXPY}=S_{MXQ}+S_{MYN}\) nên SMXPY = \(\dfrac{1}{2}S\).
Vậy SMXPY = \(\dfrac{1}{2}S\).

GV
Giáo viên Toán
Giáo viên
29 tháng 4 2017
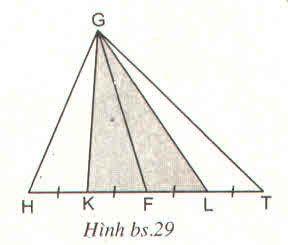
a) dt(ABMD) = dt(ABCD) - dt(CMD)
Mà dt(CMD) = 1/2 MC.h = 1/2 . 2/3 . BC .h = 1/3 dt(ABCD) = 1/3.S
(với h là đường cao hạ từ A xuống BC của hình bình hành ABCD)
Suy ra dt(ABMD) = S - 1/3 S = 2/3. S
b) dt(ABNT) = BN.h = 2/3 BC . h = 2/3 . S



* Phương án đúng:
(D). S
* Giải thích:
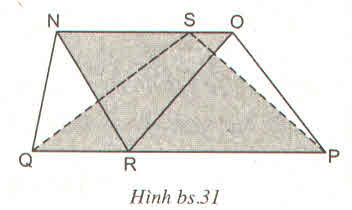
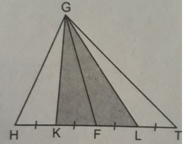
Đường cao của hình thang cũng chính bằng độ dài đường cao của hai tam giác QSP và NRO.
Gọi độ dài đường cao là h (h>0)
SQSP= \(\dfrac{1}{2}.h.QP\)
SNRO= \(\dfrac{1}{2}.h.NO\)
SNRO+SQSP=\(\dfrac{1}{2}.h.NO\)+\(\dfrac{1}{2}.h.QP\)= \(\dfrac{1}{2}.h.\left(NO+QP\right)\) (1)
Ta có:
SNOPQ=S=\(\left(NO+QP\right).h.\dfrac{1}{2}\) (2)
Từ (1) và (2) => SNRO+SQSP=S=\(\dfrac{1}{2}.h.\left(NO+QP\right)\)
* Phương án đúng:
(D). S