Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: BE+AE=BA
DF+FC=DC
mà BA=DC
và AE=FC
nên BE=DF
Ta có: AN+ND=AD
CM+MB=CB
mà AD=CB
và AN=CM
nên ND=MB
Xét ΔANE và ΔCMF có
AN=CM
\(\widehat{A}=\widehat{C}\)
AE=CF
Do đó: ΔANE=ΔCMF
Suy ra: NE=MF
Xét ΔEBM và ΔFDN có
EB=FD
\(\widehat{B}=\widehat{D}\)
BM=DN
Do đó: ΔEBM=ΔFDN
Suy ra: EM=FN
Xét tứ giác MENF có
ME=NF
NE=MF
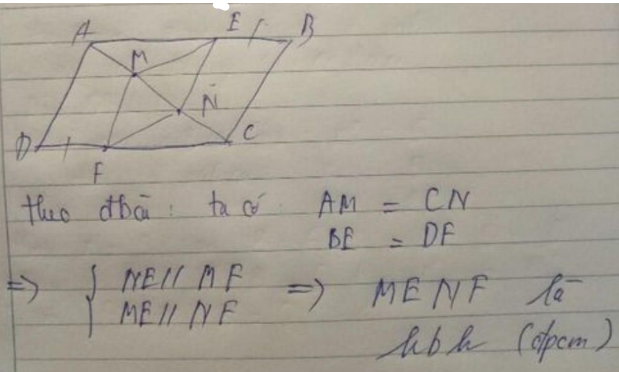
Do đó: MENF là hình bình hành

Ta có: BE+AE=BA
DF+FC=DC
mà BA=DC
và AE=FC
nên BE=DF
Ta có: AN+ND=AD
CM+MB=CB
mà AD=CB
và AN=CM
nên ND=MB
Xét ΔANE và ΔCMF có
AN=CM
\(\widehat{A}=\widehat{C}\)
AE=CF
Do đó: ΔANE=ΔCMF
Suy ra: NE=MF
Xét ΔEBM và ΔFDN có
EB=FD
\(\widehat{B}=\widehat{D}\)
BM=DN
Do đó: ΔEBM=ΔFDN
Suy ra: EM=FN
Xét tứ giác MENF có
ME=NF
NE=MF
Do đó: MENF là hình bình hành

a: Ta có: BE+AE=BA
DF+FC=DC
mà BA=DC
và AE=FC
nên BE=DF
Ta có: AN+ND=AD
CM+MB=CB
mà AD=CB
và AN=CM
nên ND=MB
Xét ΔANE và ΔCMF có
AN=CM
\(\widehat{A}=\widehat{C}\)
AE=CF
Do đó: ΔANE=ΔCMF
Suy ra: NE=MF
Xét ΔEBM và ΔFDN có
EB=FD
\(\widehat{B}=\widehat{D}\)
BM=DN
Do đó: ΔEBM=ΔFDN
Suy ra: EM=FN
Xét tứ giác MENF có
ME=NF
NE=MF
Do đó: MENF là hình bình hành

Gọi O là giao điểm 2 đường chéo AC và BD
Xét \(\Delta\)AOE và \(\Delta\)COF có:AO=OC ( vì ABCD là hình bình hành ),CF=AE ( giả thiết ),^AOE=^COF ( đối đỉnh )
a
Vì vậy \(\Delta AOE=\Delta COF\left(c.g.c\right)\Rightarrow OE=OF\left(1\right)\)
Xét \(\Delta\)BON và \(\Delta\)DOM có:OB=OD ( vì ABCD là hình bình hành ),MD=BN ( vì AM=CN ),^MOD=^NOB ( đối đỉnh )
Vì vậy \(\Delta BON=\Delta COM\left(c.g.c\right)\Rightarrow OM=ON\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) suy ra tứ giác EMFN là hình bình hành.
b
Hình bình hành EMFN có O là giao điểm của 2 đường chéo,tứ giác ABCD có O là giao điểm của 2 đường chéo.
=> ĐPCM
P/S:Mik ko chắc lắm đâu nha,nhất là câu b ý:p