Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

.a.
Vì `EF` là đường trung trực MB.
=> `EM=EB`
=> `ΔEMB` cân tại E
=> \(\widehat{EMB}=\widehat{EBM}\)
Chứng minh tương tự được: \(\widehat{FMB}=\widehat{FBM}\)
Vì `AM=DN` mà AM//DN
=> Tứ giác `AMND` là hình bình hành.
b.
Từ câu (a) suy ra:
ME//BF
BE//FM
=> Hình bình hành MEBF có `EF⊥MB`
=> Tứ giác MEBF là hình thoi

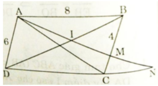
a) AD // BC (gt)![]()
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
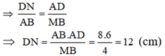
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
![]()
Tương tự, do AD // BM nên
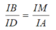
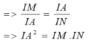

5:
5.1: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
AB=AC
Do đó: ABDC là hình thoi
5.2: Xét tứ giác DMEC có
K là trung điểm chung của DE và MC
=>DMEC là hình bình hành
=>DM//ECvà DM=EC
mà AM=MD và A,M,D thẳng hàng
nên MA//EC và MA=EC
ΔABC cân tại A có AM là trung tuyến
nên AM vuông góc BC
Xét tứ giác AMCE có
AM//CE
AM=CE
góc AMC=90 độ
Do đó: AMCE là hình chữ nhật
5.3:
AMCE là hình chữ nhật
=>AE//CM và AE=CM
mà B,M,C thẳng và MB=MC
nên MB//AE và MB=AE
=>AEMB là hình bình hành
=>AM cắt EB tại trung điểm của mỗi đường
=>I là trung điểm của BE