Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBEF và ΔDEA có
góc BEF=góc DEA
góc EBF=góc EDA
=>ΔBEF đồng dạng với ΔDEA
b: Xét ΔEAB và ΔEGD có
góc EAB=góc EGD
góc AEB=góc GED
=>ΔEAB đồng dạng với ΔEGD
=>EA/EG=EB/ED
=>EA*ED=EB*EG

a) Xét tam giác BEF và tam giác DEA có:
góc BEF = góc AED (đối đỉnh);
góc ADE = góc EBF (ở vị trí so le trong của AD song song với BC "ABCD là hình bình hành")
=> tam giác BEF đồng dạng với tam giác DEA (g-g)
Xét tam giác DGE và tam giác BAE có:
góc DEG = góc AEB (đối đỉnh);
góc EDG = góc ABE (vị trí so le trong của AB song song với CD "ABCD là hình binh hành")
=> tam giác DGE đồng dạng với tam giác BAE (g-g)
b) tam giác BEF đồng dạng với tam giác DEA
=> \(\dfrac{BE}{DE}=\dfrac{EF}{EA}\left(1\right)\)
Tam giác BAE đồng dạng với tam giác DGE
=> \(\dfrac{BE}{DE}=\dfrac{AE}{GE}\left(2\right)\)
Từ (1)(2) => \(\dfrac{EF}{EA}=\dfrac{AE}{GE}\Leftrightarrow EF.EG=AE^2\)

a: Xét ΔBEF và ΔDEA có
góc BEF=góc DEA
góc EBF=góc EDA
=>ΔBEF đồng dạng với ΔDEA
Xet ΔDGE và ΔBAE có
góc EDG=góc EBA
góc DEG=góc BEA
=>ΔDGE đồng dạng với ΔBAE
b: ΔBEF đồng dạng với ΔDEA
=>EB/ED=EF/EA
=>EA*EB=ED*EF
=>EA=ED*EF/EB
ΔDGE đồng dạng với ΔBAE
=>ED/EB=EG/EA
=>ED*EA=EB*EG
=>EA=EB*EG/ED
=>EA^2=EF*EG

Câu 2: pt đã cho \(\Leftrightarrow x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1=x^3+6x^2+12x+8\)
\(\Leftrightarrow2x^3-6x^2-6x-8=0\)
\(\Leftrightarrow x^2-3x^2-3x-4=0\)
\(\Leftrightarrow\left(x-1\right)^3-6\left(x-1\right)-9=0\) (*)
Đặt \(x-1=t\) thì (*) trở thành \(t^3-6t-9=0\)
\(\Leftrightarrow t^3-9t+3t-9=0\)
\(\Leftrightarrow t\left(t^2-9\right)+3\left(t-3\right)=0\)
\(\Leftrightarrow\left(t-3\right)\left(t^2+3t\right)+3\left(t-3\right)=0\)
\(\Leftrightarrow\left(t-3\right)\left(t^3+3t+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=3\\t^2+3t+3=0\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x-1=3\)
\(\Leftrightarrow x=4\)
Vậy pt đã cho có nghiệm \(x=4\)
bài đấy thì em làm được rồi á. Chỉ là em đăng lên xem còn cách nào giải hay hơn thôi ạ...

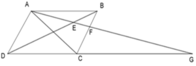
Có ABCD là hình bình hành nên: AD // BC, AB // DC
A D E ^ = F B E ^ (cặp góc so le trong)
A B E ^ = E D G ^ (cặp góc so le trong)
Xét tam giác BFE và tam giác DAE có:
A D E ^ = F B E ^ (cmt)
A E D ^ = F E B ^ (đối đỉnh)
=> ΔBFE ~ ΔDAE (g - g) nên A đúng, C sai.
Xét tam giác DGE và tam giác BAE có:
A B E ^ = E D G ^ (cmt)
A E B ^ = G E D ^ (đối đỉnh)
=> ΔDGE ~ ΔBAE (g - g) hay ΔDEG ~ ΔBEA nên B, D đúng
Đáp án: C

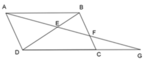
+) Vì ABCD là hình bình hành nên AD // BC => AD // BF (tính chất hbh)
Xét ΔBEF và ΔDEA có:
B E F ^ = D E A ^ (hai góc đối đỉnh)
F B E ^ = A D E ^ (cặp góc so le trong bằng nhau)
=> ΔBEF ~ ΔDEA (g - g) nên A sai
+) Vì ABCD là hình bình hành nên AB // DC => AB // DF
Xét ΔDGE và ΔBAE ta có:
D E G ^ = B E A ^ (2 góc đối đỉnh)
A B E ^ = G D E ^ (cặp góc so le trong bằng nhau)
=> ΔDGE ~ ΔBAE (g - g) nên B sai
+) Vì ΔBEF ~ ΔDEA nên E F E A = B E D E (1)
Vì ΔDGE ~ ΔBAE nên A E G E = B E D E (2)
Từ (1) và (2) ta có: E F E A = A E G E ⇔ A E 2 = GE.EF nên C đúng
Đáp án: C
Tham khảo:a) Xét tam giác BEF và tam giác DEA có:
góc BEF = góc AED (đối đỉnh);
góc ADE = góc EBF (ở vị trí so le trong của AD song song với BC "ABCD là hình bình hành")
=> tam giác BEF đồng dạng với tam giác DEA (g-g)
Xét tam giác DGE và tam giác BAE có:
góc DEG = góc AEB (đối đỉnh);
góc EDG = góc ABE (vị trí so le trong của AB song song với CD "ABCD là hình binh hành")
=> tam giác DGE đồng dạng với tam giác BAE (g-g)
b) tam giác BEF đồng dạng với tam giác DEA
=> BE/DE=EF/EA (1)
Tam giác BAE đồng dạng với tam giác DGE
=>BE/DE=AE/GE (2)
Từ (1)(2) =>EF/EA=AE/GE=> EF.EG=AE^2
c) tam giác BEF đồng dạng với tam giác DEA
=> BE/DE=BF/DA (3)
Tam giác BAE đồng dạng với tam giác DGE
=> BE/DE=BA/DG (4)
Từ (3)(4) => BF/AD=BA/DG=> BF.DG=BA.AD
Mà AB và AD là 2 cạnh của hình bình hành ABCD nên AB.AD không đổi
=> BF.DG không đổi khi F di chuyển trên BC
chj ơi cho e xem hình đc khum