Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
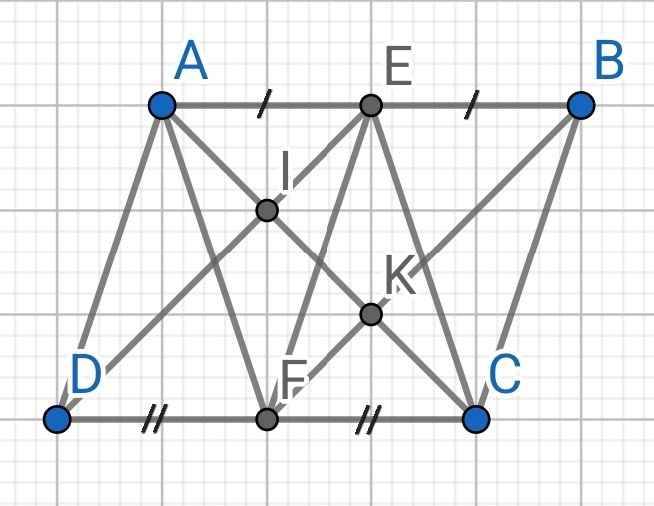a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC
ABCD là hình bình hành \(\Rightarrow\) AB = CD; góc A = góc C; AD = BC
E là trung điểm của AD \(\Rightarrow\) AE = \(\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow\) FC = \(\frac{BC}{2}\)
mà AD = BC (cmt)
nên AE = FC
Xét \(\Delta\) ABE và \(\Delta\) CDF có
góc A = góc C (cmt)
AE = FC (cmt)
AB = CD (cmt)
\(\Rightarrow\) tam giác ABE = tam giác CDF (c.g.c)
\(\Rightarrow\) BE = DF
Gọi E là trung điểm DC
Xét tam giác BDC có:
E là trung điểm DC
M là trung điểm BC
=> EM là đường trung bình
=> EM//BD
=> EM//ID
Ta có: \(AD=\dfrac{1}{2}DC\)
Mà \(DE=\dfrac{1}{2}DC\)
\(\Rightarrow AD=DE=\dfrac{1}{2}AE\)=> D là trung điểm AE
Xét tam giác AME có:
D là trung điểm AE
ID//ME
=> I là trung điểm AM
=> AI=IM
1: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
a, Xét tam giác ADC có Q là trung điểm của AD và P là trung điểm của DC => QP là đường trung bình của tam giác ADC.=> QP//AC và QP=\(\dfrac{1}{2}\)AC (1)
Xét tam giác ABC có M là trung điểm của AB và N là trung điểm của BC => MN là đường trung bình của tam giác ABC => MN//AC và MN=\(\dfrac{1}{2}\)AC (2)
Từ (1) và (2) => QP=MN và QP//MN => MNPQ là hình bình hành
b,Nếu ABCD là hình thang cân <=> AC=BD (2 đường chéo) (3)
Xét tam giác BCD có N là trung điểm của BC và P là trung điểm của DC => NP là đương trung bình của tam giác BCD => NP//BD và NP=\(\dfrac{1}{2}\)BD (4)
=> Từ (1) (3) và (4) ta có QP=NP
=> ABCD là hình bình hành có QP=NP ( cạnh kề )
=> ABCD là hình thoi
BẠN TỰ VẼ HÌNH NHA
Cho hình bình hành ABCD. Lấy M tùy ý trên cạnh DC - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
Tui không biết làm, nhưng tìm được cái đó, lấy cái đó tham khảo nha!