Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

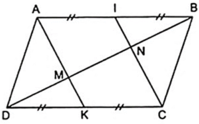
Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: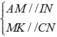
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
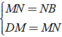 ⇒ DM = MN = NB
⇒ DM = MN = NB

Gọi o là tâm của hình bình hành.
Ta cóF;E là trọng tâm của tam giác ABC và ADC(vì AN:AM:AO;BO trung tuyến)
OE=\(\frac{OB}{3}\) và OF=\(\frac{OD}{3}\)
Vậy OE=OF(vì OB=OD) và FE=2OE=2FO(1)
F là trọng tâm của tam giác ADC nên \(\frac{FO}{FD}\)=\(\frac{1}{2}\)nên FD=2FO(2)
E là trọng tâm tam giác ABC nên \(\frac{EO}{EB}\)=\(\frac{1}{2}\)nên EB=2OE(3)
Từ(1)(2)(3) suy ra FE=FD=BE

a) AK=1/2AB; CI=1/2CD
mà AB//=CD nên AK//=CI suy ra
AKCI là hình bình hành
do đó AI//CK
b) Xét tam giác CDN
có I là trung điểm CD mà IM//CN
nên M là trung điểm DN hay DM=MN (3)
(Theo định lý đường thẳng đi qua một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba)
Tương tự xét tam giác ABM cũng có BN=MN (4)
Từ (3) và (4) suy ra DM=MN=NB

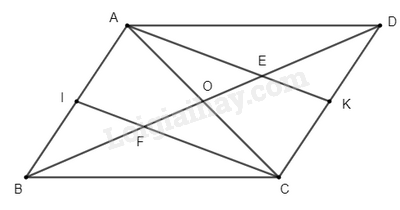
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AB\) // \(CD\), \(AD\) // \(BC\); \(AB = CD\); \(AD = BC\)
Mà \(IA = IB = \frac{{AB}}{2}\); \(KD = KC = \frac{{CD}}{2}\) (do \(I\),\(K\) là trung điểm)
Suy ra \(IA = IB = KD = KC\)
Xét tứ giác \(AKCI\) có:
\(AI = KC\) (cmt)
\(AI\) // \(KC\)
Suy ra \(AKCI\) là hình bình hành
Suy ra \(IC\) // \(AK\)
Hay \(IF\) // \(AE\)
Suy ra \(AEFI\) là hình thang
b) Vì \(ABCD\), \(AKCI\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\), \(BD\), \(KI\)
Suy ra \(OD = OB = \frac{1}{2}BD\) (1)
Xét tam giác \(ADC\) có hai trung tuyến \(AK\), \(DO\) cắt nhau tại \(E\)
Suy ra \(E\) là trọng tâm của tam giác
Suy ra \(ED = \frac{2}{3}DO\) (2)
Chứng minh tương tự ta có \(BF = \frac{2}{3}BO\) (3)
Từ (1), (2), (3) suy ra \(ED = BF = \frac{1}{3}BD\)
Suy ra \({\rm{EF}} = \frac{1}{3}BD\)
Vậy \(DE = EF = FB\)
Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.