Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

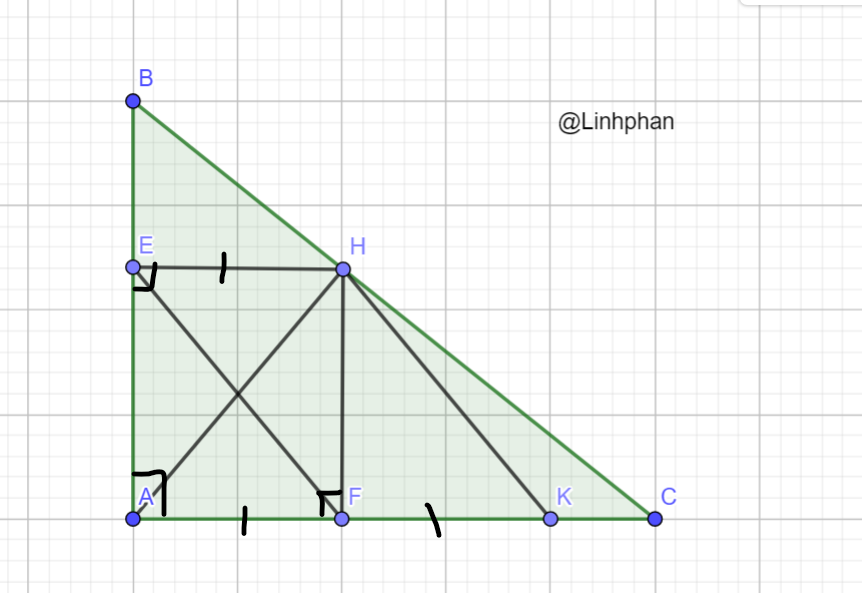
a, Vì HE ⊥ AB ; FA ⊥ AB => HE // FA (từ ⊥ đến // )
+, EA ⊥ AC ; HF ⊥ AC => EA // HF (từ ⊥ đến // )
Xét tứ giác AEHF có: HE // FA (cmt) ; EA // HF (cmt)
=> Tứ giác AEHF là hình bình hành (dhnb)
mà \(\hat{EAF} =90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> AH = EF
b, Vì AEHF là hình chữ nhật (cmt)
=> EH//AF; EH = AF mà AF= FK (gt)
=> EH = FK
+, Xét tứ giác EHKF có: EH = FK (cmt)
EH // FK (do EH // AF; K ∈ AF)
=> Tứ giác EHKF là hình bình hành (dhnb)

c: Ta có: ΔAHC vuông tại H
mà HF là đường trung tuyến
nên HF=AF
mà AF=ME
nên HF=ME
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: FE là đường trung bình
=>FE//BC
hay FE//MH
Xét tứ giác EFMH có FE//MH
nên EFMH là hình thang
mà FH=ME
nên EFMH là hình thang cân
d: Xét tứ giác MNAB có
MN//AB
MN=AB
Do đó: MNAB là hình bình hành
Suy ra: MA cắt NB tại trung điểm của mỗi đường(1)
Ta có: AEMF là hình chữ nhật
nên MA cắt EF tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AM,BN,FE đồng quy