Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng Talet vào tam giác AEM có AE//CD
\(\frac{AM}{CM}=\frac{1}{3}\Rightarrow\frac{AM}{AC}=\frac{1}{4}\Rightarrow S_{ADM}=\frac{1}{4}S_{ADC}=\frac{1}{8}S\)
Tương tự: \(\frac{CN}{AN}=\frac{1}{2}\Rightarrow\frac{CN}{AC}=\frac{1}{3}\Leftrightarrow S_{DNC}=\frac{1}{3}S_{ADC}=\frac{1}{6}S\)
Có: \(S_{DMN}=S_{ADC}-S_{ADM}-S_{DNC}=\frac{1}{2}S-\frac{1}{8}S-\frac{1}{6}S=\frac{5}{24}S\)

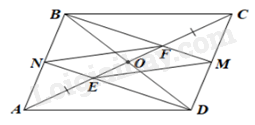
a) Ta có:
\(AE = EF = FC\) nên \(AE = EF = FC = \frac{1}{3}AC\) (1)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) hay \(OA = OC = \frac{1}{2}AC\) và \(AC = 2OA = 2OC\) (2)
Từ (1) và (2) suy ra \(AE = EF = FC = \frac{2}{3}OA = \frac{2}{3}OC\).
Xét \(\Delta BCD\) có \(CO\) là trung tuyến và \(CF = \frac{2}{3}CO\) (cmt)
Suy ra \(F\) là trọng tâm của \(\Delta BCD\)
Suy ra \(BM\) là đường trung tuyến của \(\Delta BCD\)
Suy ra \(M\) là trung điểm của \(CD\)
Xét \(\Delta ABD\) có \(AO\) là trung tuyến và \(AE = \frac{2}{3}AO\) (cmt)
Suy ra \(E\) là trọng tâm của \(\Delta ABD\)
Suy ra \(DN\) là đường trung tuyến của \(\Delta ABD\)
Suy ra \(N\) là trung điểm của \(AB\)
b) Do M là trung điểm của CD (câu a) nên \(MC = MD = \frac{1}{2}CD\).
N là trung điểm của AB (câu a) nên \(NB = NA = \frac{1}{2}AB\).
Mà AB = CD và AB // CD (do ABCD là hình bình hành)
Suy ra NB = MD và NB // MD.
Xét tứ giác BMDN có NB = MD và NB // MD
Do đó BMDN là hình bình hành.
Suy ra BM // DN và BM = DN.
Ta có E là trọng tâm của DABD nên \(EN = \frac{1}{3}DN\).
F là trọng tâm của DBCD nên \(FM = \frac{1}{3}BM\).
Mà DN = BM (chứng minh trên) nên EN = FM.
Xét tứ giác EMFN có EN = FM và EN // FM (do BM // DN)
Suy ra EMFN là hình bình hành.

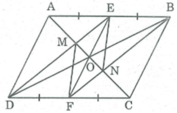
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).