Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) ΔABC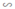 
ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔABC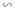 
ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHBA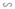 
ΔHAC vì cùng đồng dạng với ΔABC.
b) + ΔABC vuông tại A
⇒ BC2 = AB2 + AC2
(Theo định lý Pytago)
4.2:
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
góc ABH=góc BDC
=>ΔAHB đồng dạng với ΔBCD
b: BD=căn 9^2+12^2=15cm
AH=9*12/15=108/15=7,2cm
c: HB=AB^2/BD=12^2/15=9,6cm
S AHB=1/2*AH*HB=1/2*7,2*9,6=34,56cm2
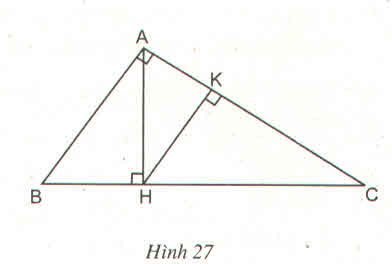
Các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng:
-
△
ABC đồng dạng
△
HBA. Ta có: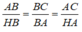 
-
△
ABC đồng dạng
△
HAC. Ta có: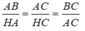 
-
△
ABC đồngdạng
△
KHC. Ta có: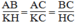 
-
△
ABC đồng dạng
△
KAH. Ta có: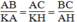 
-
△
HBA đồng dạng
△
HAC. Ta có: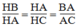 
-
△
HBA đồng dạng
△
KHC. Ta có: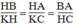 
-
△
HBA đồng dạng
△
KAH. Ta có: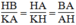 
-
△
HAC đồng dạng
△
KHC.Ta có: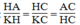 
-
△
HAC đồng dạng
△
KAH. Ta có: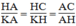 
-
△
KHC đồngdạng
△
KAH. Ta có: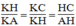 
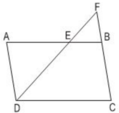
a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB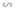 
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB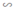 
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA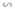 
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB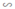 
ΔDEA
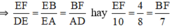
⇒ EF = 5cm, BF = 3,5cm.
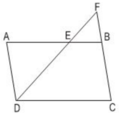
a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB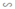 
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB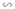 
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA 
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB 
ΔDEA
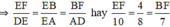
⇒ EF = 5cm, BF = 3,5cm.
- △ ABC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ở đỉnh B chung
- △ ABC đồng dạng △ HAC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ ABC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ∠ (HBA) = ∠ (HAC)
- △ HAB đồng dạng △ NCM
Hai tam giác vuông có góc nhọn ∠ (HAB) = ∠ (NCM)
a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB - AE = 12 - 8 = 4cm
∆ADE ∽ ∆BFE => =
=
=> =
=
=> BF = 3,5 cm.
EF = 5 cm.
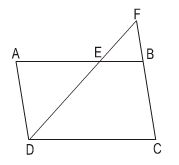
a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB – AE = 12 – 8 = 4cm
∆ADE ∽ ∆BFE =>\(\frac{AE}{BE}=\frac{AD}{BF}=\frac{DE}{EF}\)
\(\Rightarrow\frac{8}{4}=\frac{7}{BF}=\frac{10}{EF}\)
\(\Rightarrow BF=3,5cm\)
\(\Rightarrow EF=5cm\)
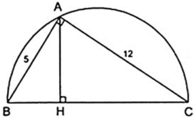
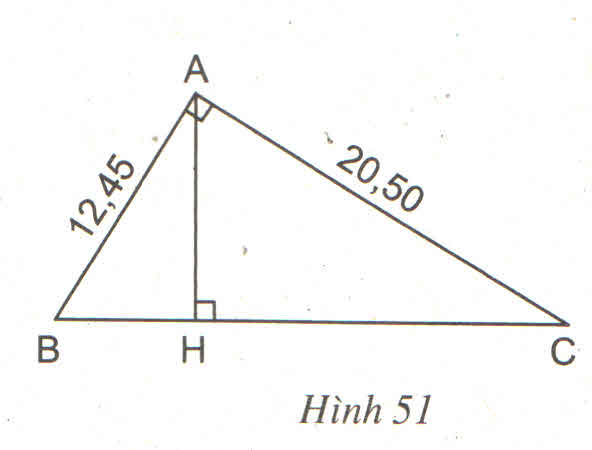
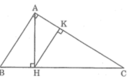
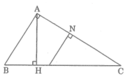
Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.