Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
a) Thế x = 4 và y = 11 vào y = 3x +b ta có: 11 = 3.4 + b ⇔ b = -1. Khi đó hàm số đã cho trở thành: y = 3x – 1. Đây là đường thẳng đi qua 2 điểm A(0;-1) và B(1/3; 0)
b) Đồ thị hàm số y = ax + 5 đi qua điểm A(-1; 3) nên: 3 = a(-1) + 5
<=> a = 2
Khi đó hàm số đã cho trở thành : y = 2x + 5. Đây là đường thẳng đi qua hai điểm A(0; 5) và B (−52;0)(−52;0)
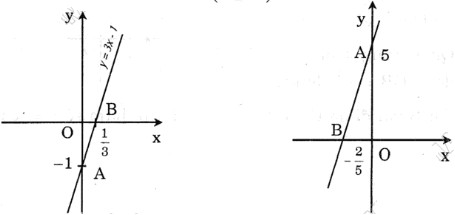

Để hàm số y=(m-5)x là hàm số bậc nhất thì \(m-5\ne0\)
hay \(m\ne5\)
1) Để hàm số y=(m-5)x đồng biến trên R thì m-5>0
hay m>5
Để hàm số y=(m-5)x nghịch biến trên R thì m-5<0
hay m<5
2) Để đồ thị hàm số y=(m-5)x đi qua A(1;2) thì
Thay x=1 và y=2 vào hàm số y=(m-5)x, ta được:
m-5=2
hay m=7(nhận)
Vậy: Để đồ thị hàm số y=(m-5)x đi qua A(1;2) thì m=7


Lời giải
a) Hàm số bậc nhất đồng biến khi (a>0) => m-3 >0 => m>3
b) A(1;2) => y(1) =2 => (m-3).1=2 => m=5
c) B(1;-2) => y(1) =-2=> (m-3).1=-2 => m=1
d)
a) Hàm số \(y=\left(m-3\right)x\) đồng biến khi \(m-3>0\Leftrightarrow m>3\)
Hàm số \(y=\left(m-3\right)x\) nghịch biến khi \(m-3< 0\Leftrightarrow m< 3\)