
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

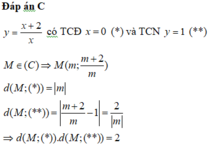

Đáp án C
Tiệm cận đứng: d 1 : x = - 1 , tiệm cận ngang d 2 : y = 1 suy ra tâm đối xứng là I ( - 1 ; 1 ) . Phương trình tiếp tuyến tại M a ; a + 2 a + 1 ∈ ( C ) a ≠ - 1 là: y = - 1 ( a + 1 ) 2 x - a + a + 2 a + 1 d
Khi đó d I ; d = - 1 a + 1 2 - 1 - a - 1 + a + 2 a + 1 1 a + 1 4 + 1 = 2 a + 1 1 a + 1 4 + 1 = 2 1 a + 1 2 + a + 1 2 ≤ 2 2 1 a + 1 2 . a + 1 2 . Hay d ≤ 2 2 = 2 .

Chọn C.
Phương pháp: Viết phương trình tiếp tuyến và tính khoảng cách, sau đó sử dụng điều kiện có nghiệm để tìm giá trị lớn nhất.

Tọa độ giao điểm của hai đường tiệm cận của (C) là I(-1;1)
Ta có:


Đáp án C
Ta có y ' = - 1 x - 2 2 . Gọi M a ; 2 a - 3 a - 2 là tọa độ tiếp điểm của tiếp tuyến
Hệ số góc của tiếp tuyến là k = y ' a = - 1 a - 2 2
Phương trình đường thẳng d là y = - 1 a - 2 2 x - a + 2 a - 3 a - 2
Đồ thị hàm số có tiệm cận đứng là x = 2 tiệm cận ngang là y = 2
Ta có A 2 ; 2 a - 2 a - 2 , B 2 a - 2 ; 2 ⇒ A B = 4 a - 2 2 + 4 a - 2 2 = 2 a - 2 2 + 1 a - 2 2
Áp dụng bất đẳng thức Cô-si ta có A B = 2 a - 2 2 + 1 a - 2 2 ≥ 2 2 a - 2 2 . 1 a - 2 2 = 2 2
Do đó khoảng cách ngắn nhất giữa A và B là 2 2 .

Đáp án C
Gọi M x 0 ; 2 x 0 − 3 x 0 − 2 là tiếp tuyến của d với (C)
Ta có y ' = − 1 x − 2 2 ⇒ y ' x 0 = − 1 x 0 − 2 2
Suy ra d : y = − 1 x 0 − 2 2 x − x 0 + 2 x 0 − 3 x 0 − 2 ⇔ d : y = − 1 x 0 − 2 2 x + 2 x 0 2 − 6 x 0 + 6 x 0 − 2 2
Ta có d ∩ x = 2 = A 2 ; 2 x 0 − 2 x 0 − 2 d ∩ y = 2 = B 2 x 0 − 2 ; 2 ⇒ A B = 4 x 0 − 2 2 + 4 x 0 − 2 2
Có A B 2 = 4 x 0 − 2 2 + 4 x 0 − 2 2 ≥ 24 x 0 − 2 2 4 x 0 − 2 2 = 8 ⇒ A B ≥ 2 2 ⇒ min A B = 2 2

Đáp án C
Phương pháp :
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2
y = f’(m – 2)(x – m +2)+y(m – 2) (d)
+) Xác định các giao điểm của d và các đường tiệm cận => x2;y1
+) Thay vào phương trình x2 + y1 = –5 giải tìm các giá trị của m.
Cách giải: TXĐ: D = R\ {–2}
Ta có 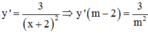
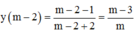
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2 là: 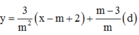
Đồ thị hàm số y = x - 1 x + 2 có đường TCN y = 1và tiệm cậm đứng x = –2
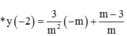
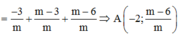
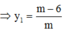
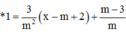
![]()
![]()
![]()
![]()
![]()
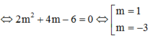
![]()

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!