Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Tiệm cận đứng: d 1 : x = - 1 , tiệm cận ngang d 2 : y = 1 suy ra tâm đối xứng là I ( - 1 ; 1 ) . Phương trình tiếp tuyến tại M a ; a + 2 a + 1 ∈ ( C ) a ≠ - 1 là: y = - 1 ( a + 1 ) 2 x - a + a + 2 a + 1 d
Khi đó d I ; d = - 1 a + 1 2 - 1 - a - 1 + a + 2 a + 1 1 a + 1 4 + 1 = 2 a + 1 1 a + 1 4 + 1 = 2 1 a + 1 2 + a + 1 2 ≤ 2 2 1 a + 1 2 . a + 1 2 . Hay d ≤ 2 2 = 2 .

Chọn C.
Phương pháp: Viết phương trình tiếp tuyến và tính khoảng cách, sau đó sử dụng điều kiện có nghiệm để tìm giá trị lớn nhất.

Tọa độ giao điểm của hai đường tiệm cận của (C) là I(-1;1)
Ta có:


Đáp án B
Sai lầm thường gặp: Tập xác định D = ℝ \ 3 .
Đạo hàm y ' = − 2 x − 3 2 ,0, ∀ x ∈ D ⇒ Hàm số nghịch biến trên ℝ \ 3 , hoặc làm số nghịch biến trên − ∞ ; 3 ∪ 3 ; + ∞ . Hàm số không có cực trị.
Tiệm cận đứng: x=3; tiệm cận ngang: y=1. Đồ thị hàm số nhận giao điểm I 3 ; 1 của hai đường tiệm cận làm tâm đối xứng.
Từ đó nhiều học sinh kết luận các mệnh đề 1 , 3 , 4 đúng và chọn ngay A.
Tuy nhiên đây là phương án sai.
Phân tích sai lầm:
Mệnh đề (1) sai, sửa lại: hàm số nghịch biến trên mỗi khoảng − ∞ ; 3 và 3 ; + ∞ . Học sinh cần nhớ rằng, ta chỉ học định nghĩa hàm số đồng biến (nghịch biến) trên khoảng, đoạn, nửa khoảng; chứ không có trên những khoảng hợp nhau.
Mệnh đề (2) sai. Đồ thị hàm số có một tiệm cận đứng là x=3, một tiệm cận ngang là y=1.
Mệnh đề 3 , 4 đúng.

Chọn C.
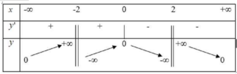
Phương pháp: Dựa vào bảng biến thiên để xác định tiệm cận, cực trị, giá trị lớn nhất, giá trị nhỏ nhất.
Cách giải: Dựa vào bảng biến thiên dễ thấy đồ thị hàm số có tiệm cận ngang y = 0 và hai tiệm cận đứng x = 2, x = -2. Vậy (I) sai và (IV) đúng.


Đáp án C
Phương pháp :
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2
y = f’(m – 2)(x – m +2)+y(m – 2) (d)
+) Xác định các giao điểm của d và các đường tiệm cận => x2;y1
+) Thay vào phương trình x2 + y1 = –5 giải tìm các giá trị của m.
Cách giải: TXĐ: D = R\ {–2}
Ta có 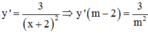
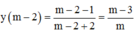
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2 là: 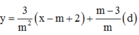
Đồ thị hàm số y = x - 1 x + 2 có đường TCN y = 1và tiệm cậm đứng x = –2
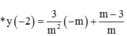
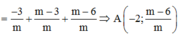
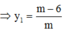
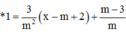
![]()
![]()
![]()
![]()
![]()
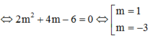
![]()

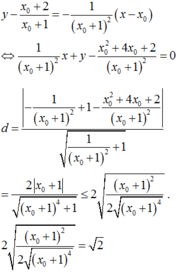

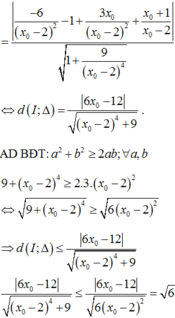


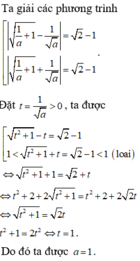
Đáp án A
Ta có: I 3 2 ; 1 2 . PTTT tại điểm M bất kì là: y = − 1 2 x 0 − 3 2 x − x 0 + x 0 − 1 2 x 0 − 3 Δ
Khi đó: d I ; Δ = 1 2 2 x 0 − 3 + x 0 − 1 2 x 0 − 3 − 1 2 1 2 x 0 − 3 + 1 = 1 1 2 x 0 − 3 2 + 2 x 0 − 2 2 ≤ 1 2