Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
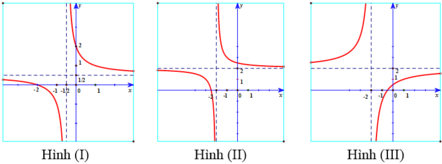
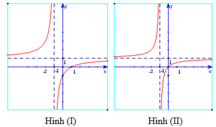
Hàm số y = x - m 2 - 1 x + 1 có tập xác định D = ℝ \ { - 1 }
y ' = m 2 + 2 ( x + 1 ) 2 suy ra y ' > 0 ∀ m , và y = x - m 2 - 1 x + 1 đi qua điểm 0 ; - 1 .
Hình (I) đúng.
Hình (II) sai vì không đi qua điểm 0 ; - 1 .
Hình (III) sai vì không đi qua điểm 0 ; - 1 .

Chọn D
Ta có

Vì f'(x) luôn đồng biến trên
ℝ
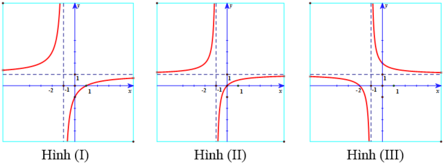
nên ![]() , do đó: a > 0 và b > 0
, do đó: a > 0 và b > 0
Mặt khác vì đồ thị hàm số không cắt trục Ox nên chọn đáp án D.

Phương pháp:
Sử dụng cách đọc đồ thị hàm số.
Cách giải:
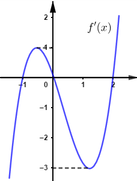
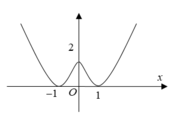
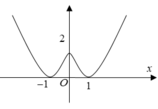
Từ đồ thị hàm số ta thấy
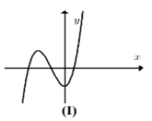
+ Đồ thị đi xuống trên khoảng 0;1
nên Hàm số nghịch biến trên
khoảng 0;1. Do đó (I) đúng
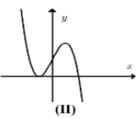
+ Đồ thị đi lên trên khoảng 1;0,
đi xuống trên khoảng 0;1và đi
lên trên khoảng 1;2 nên trên
khoảng 1;2 hàm số không
hoàn toàn đồng biến. Do đó (II) sai.
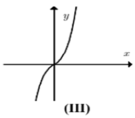
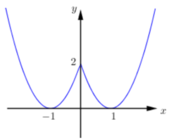
+ Đồ thị hàm số có ba điểm hai
điểm cực tiểu và một điểm cực
đại nên (III) đúng.
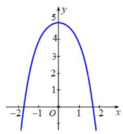
+ Giá trị lớn nhất của hàm số là
tung độ của điểm cao nhất của đồ
thị hàm số nên (IV) sai.
Như vậy ta có hai mệnh đề đúng
là (I) và (III).
Chọn B.


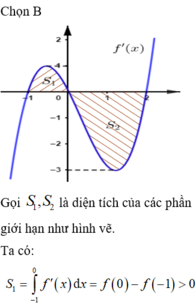
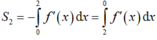
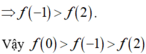
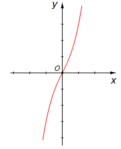


Chọn D.
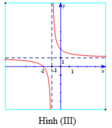
Hàm số y = m x + 1 x + m có tập xác định D = ℝ \ - m . Ta có y ' = m 2 - 1 ( x + m ) 2 , y ' < 0 ⇔ m 2 - 1 < 0 ⇔ - 1 < m < 1 ; y ' > 0 ⇔ m 2 - 1 > 0 ⇔ [ m > 1 m < - 1 . Hình (I) có m = - 1 2 ∈ - 1 ; 1 nên y ' > 0 suy ra hàm số nghịch biến, do đó Hình (I) đúng. Hình (II) có m = - 3 2 < - 1 nên y ' < 0 suy ra hàm số đồng biến, do đó Hình (II) sai. Hình (III) có m = - 2 < - 1 nên y ' > 0 suy ra hàm số đồng biến, do đó Hình (III) đúng.