PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
21 tháng 11 2017
Vẽ đồ thị hàm số
| x | -2 | -1 | 0 | 1 | 2 |
| y = 0,5 x 2 | 2 | 0,5 | 0 | 0,5 | 2 |
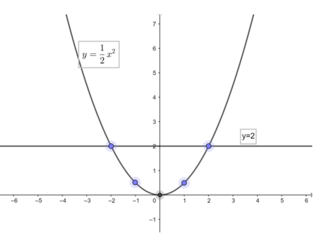
Dựa vào đồ thị ta thấy:
Khi -2 < x < 2 thì 0 ≤ y ≤ 2
PT
1
CM
28 tháng 1 2018
Vẽ đồ thị hàm số
| x | -2 | -1 | 0 | 1 | 2 |
| y = 0,5 x 2 | 2 | 0,5 | 0 | 0,5 | 2 |
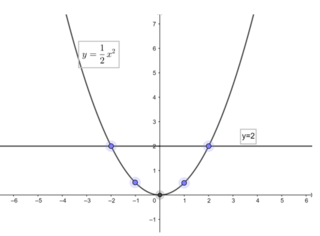
Dựa vào đồ thị ta thấy:
Khi x ≤ 0 thì y ≥ 0
PT
1
CM
28 tháng 2 2018
Vẽ đồ thị hàm số
| x | -2 | -1 | 0 | 1 | 2 |
| y = 0,5 x 2 | 2 | 0,5 | 0 | 0,5 | 2 |
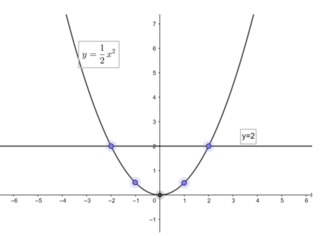
Dựa vào đồ thị ta thấy:
Để giá trị y < 2 thì -2 < x < 2
PT
1
CM
25 tháng 6 2018
Vẽ đồ thị hàm số
| x | -2 | -1 | 0 | 1 | 2 |
| y = 0,5 x 2 | 2 | 0,5 | 0 | 0,5 | 2 |
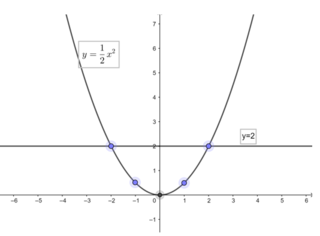
Dựa vào đồ thị ta thấy:
Để giá trị y > 2 thì x > 2 hoặc x < -2
24 tháng 10 2021
a, Vì \(5-3\sqrt{2}>0\) nên hs đồng biến trên R
b, \(x=5+3\sqrt{2}\Leftrightarrow y=25-18+\sqrt{2}-1=6+\sqrt{2}\)
c, \(y=0\Leftrightarrow\left(5-3\sqrt{2}\right)x+\sqrt{2}-1=0\Leftrightarrow x=\dfrac{1-\sqrt{2}}{5-3\sqrt{2}}\)
\(\Leftrightarrow x=\dfrac{\left(1-\sqrt{2}\right)\left(5+3\sqrt{2}\right)}{7}=\dfrac{-2\sqrt{2}-1}{7}\)
15 tháng 11 2023
a: f(5)=75/2
=>\(a\cdot5^2=\dfrac{75}{2}\)
=>\(a=\dfrac{75}{2}:25=\dfrac{3}{2}\)
Vậy: \(y=f\left(x\right)=\dfrac{3}{2}x^2\)
Khi x=-3 thì \(y=\dfrac{3}{2}\left(-3\right)^2=\dfrac{3}{2}\cdot9=\dfrac{27}{2}\)
b: y=15
=>\(\dfrac{3}{2}x^2=15\)
=>\(x^2=10\)
=>\(x=\pm\sqrt{10}\)
25 tháng 12 2023
Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)
Vẽ đồ thị hàm số
Dựa vào đồ thị ta thấy:
Khi x ≤ 2 thì y ≥ 0