Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(f'\left(x\right)=x^2-2x-3\)
\(f'\left(x\right)\le0\\ \Rightarrow x^2-2x-3\le0\\ \Leftrightarrow\left(x+1\right)\left(x-3\right)\le0\\ \Leftrightarrow-1\le x\le3\)

Đáp án C.
- Phương pháp:
+) Tính f'(x).
+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.
- Cách giải:
+ Ta có:
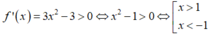
→ Vậy tập nghiệm của bất phương trình là 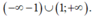

\(f'\left(x\right)=\left(x^2e^{-2x}\right)'=2x\cdot e^{-2x}-2x^2e^{-2x}\\ f'\left(x\right)=0\\ \Rightarrow2xe^{-2x}-2x^2e^{-2x}=0\\ \Leftrightarrow2xe^{-2x}\cdot\left(1-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

Chọn C.
Vì: f’(x) = 15(x + 1)2 + 4 ;
f”(x) = 30(x + 1) ⇔ f”(x) = 0 ⇔ x = -1.

Đáp án C
Ta có : f ' ( x ) = 15 ( x + 1 ) 2 + 4 ;
f ' ' ( x ) = 30 ( x + 1 ) ⇒ f ' ' ( x ) = 0 ⇔ 30 ( x + 1 ) = 0 ⇔ x = - 1 .

Đặt \(g\left(x\right)=f\left(x+\dfrac{1}{3}\right)-f\left(x\right)\)
Hiển nhiên \(g\left(x\right)\) cũng liên tục trên R
Ta có: \(g\left(0\right)=f\left(\dfrac{1}{3}\right)-f\left(0\right)\)
\(g\left(\dfrac{2}{3}\right)=f\left(1\right)-f\left(\dfrac{2}{3}\right)\)
\(g\left(\dfrac{1}{3}\right)=f\left(\dfrac{2}{3}\right)-f\left(\dfrac{1}{3}\right)\)
Cộng vế với vế:
\(g\left(0\right)+g\left(\dfrac{1}{3}\right)+g\left(\dfrac{2}{3}\right)=f\left(1\right)-f\left(0\right)=0\)
- Nếu tồn tại 1 trong 3 giá trị \(g\left(0\right);g\left(\dfrac{1}{3}\right);g\left(\dfrac{2}{3}\right)\) bằng 0 thì hiển nhiên pt có nghiệm
- Nếu cả 3 giá trị đều khác 0 \(\Rightarrow\) tồn tại ít nhất 2 trong 3 giá trị \(g\left(0\right)\) ; \(g\left(\dfrac{1}{3}\right)\) ; \(g\left(\dfrac{2}{3}\right)\) trái dấu
\(\Rightarrow\) Luôn tồn tại ít nhất 1 trong 3 tích số: \(g\left(0\right).g\left(\dfrac{1}{3}\right)\) ; \(g\left(0\right).g\left(\dfrac{2}{3}\right)\) ; \(g\left(\dfrac{1}{3}\right).g\left(\dfrac{2}{3}\right)\) âm
\(\Rightarrow\) Pt \(g\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left[0;1\right]\)
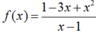
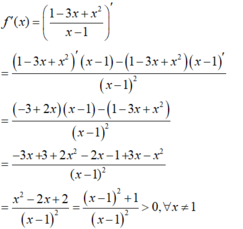
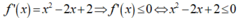

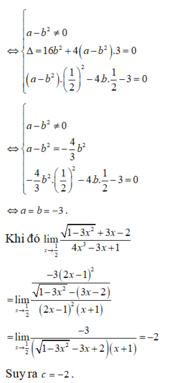
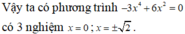
Chọn D.