Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
f(x) = x ( x- 1) \(\ge\)-1/4 với mọi x \(\in\)(0; 1]
+) f(x+1) = 2f(x) = 2x(x-1) với mọi x \(\in\)(0; 1]
=> f(x) = 2(x-1) (x- 2) với mọi x \(\in\)( 1; 2]
=> f(x) = 2(x-1) (x- 2) \(\ge\)-1/2 với mọi x \(\in\)( 1; 2]
+) f(x + 1 ) = 2 f(x) = 4 ( x - 1 ) ( x - 2 ) với x \(\in\)( 1; 2]
=> f (x ) = 4 ( x - 2 ) ( x - 3 ) với mọi x \(\in\)( 2; 4 ]
=> f (x ) = 4 ( x - 2 ) ( x - 3 ) \(\ge\)-1 với mọi x \(\in\)( 2; 3 ]
dấu bằng xảy ra tại x = 5/2 điểm cực tiểu
mà theo để ra tìm m để \(f\left(x\right)\ge-\frac{8}{9}\)với mọi x ( - \(\infty\); m ]
=>2< m < 5/2 và f(m) = -8/9
<=> m = 7/3
[URL=http://www.mediafire.com/view/corexjfrbst6qsw/f%2528x%252B1%2529.jpg/file][IMG]https://www.mediafire.com/convkey/6ebc/corexjfrbst6qsw4g.jpg[/IMG][/URL]
Em vẫn chưa hiểu phần trong khung đỏ , tại sao từ
f(x+1) = 2f(x) = 4(x-1)(x-2) với x thuộc [1.2]
ta lại suy ra được f(x) =4(x-2)(x-3) >= -1 với mọi x thuộc [2,3]
Thầy cô giải thích thêm giùm em được không ạ ,em cám ơn thầy cô nhiều

đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.

a/ ĐK x>0
\(log_{2017}x+log_{2016}x=0\Leftrightarrow\dfrac{lnx}{ln2017}+\dfrac{lnx}{ln2016}=0\)
\(\Leftrightarrow lnx\left(\dfrac{1}{ln2017}+\dfrac{1}{ln2016}\right)=0\Leftrightarrow lnx=0\Rightarrow x=1\)
b/ ĐK \(\left\{{}\begin{matrix}x-1>0\\x-1\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>1\\x\ne2\end{matrix}\right.\)
\(x^3-5x^2+6x=0\Leftrightarrow x\left(x^2-5x+6\right)=0\Rightarrow\left[{}\begin{matrix}x=0\left(l\right)\\x=2\left(l\right)\\x=3\end{matrix}\right.\) \(\Rightarrow x=3\)
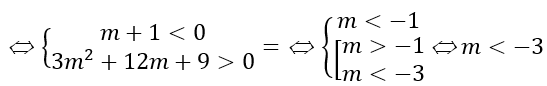
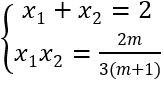
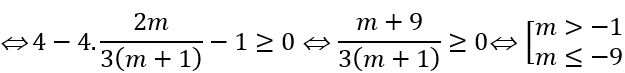
Đáp án C