Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương pháp : Chuyển vế, lấy nguyên hàm hai vế.
Cách giải :
![]()
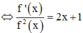
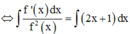
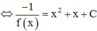
![]()
![]()
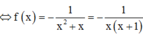
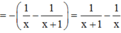
![]()
![]()
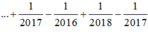
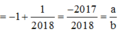
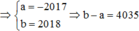

Đáp án D
Ta thấy f'(x) =0 tại x=3,x=1 nhưng chỉ đổi dấu qua x = 3 nên hàm số có đúng 1 cực trị

Phương pháp:
- Lấy nguyên hàm hai vế từ đẳng thức đạo hàm và kết hợp điều kiện tìm f(x)
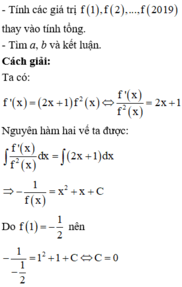


Vì

nên tích phân cần tính bằng tích phân từng phần
Ta có
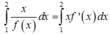
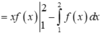
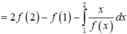
=2c-b-a
Chọn đáp án A.


⇒ ∫ 1 x f ' x 1 + f x 2 f x 4 d x = ∫ 1 x x − 1 2 d x , ∀ x ∈ 1 ; 3 ⇔ ∫ 1 x 1 f x 4 + 2 f x 3 + 1 f x 2 d f x = x − 1 3 3 x 1 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x x 1 = x − 1 3 3 − 0 3 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x − − 1 3 f 1 3 − 2 2 f 1 2 − 1 f 1 = x − 1 3 3 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x − 1 3 − 1 + 1 = x − 1 3 3 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x = x − 1 3 + 1 3 ⇔ 1 3 − 1 f x 3 − − 1 f x 2 + − 1 f x = 1 3 x 3 − x 2 + x ( * )


Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
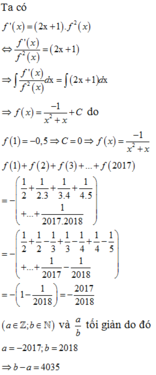
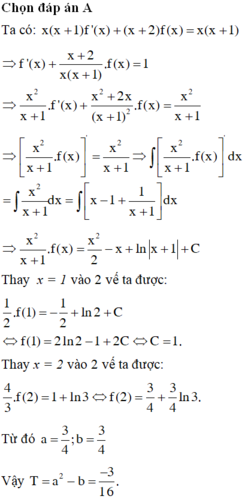
Đáp án D